题目内容
10.P为双曲线$\frac{x^2}{4}-\frac{y^2}{9}=1$右支上一点,F1,F2分别为双曲线的左右焦点,且$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$,直线PF2交y轴于点A,则△AF1P的内切圆半径为( )| A. | 2 | B. | 3 | C. | $\frac{3}{2}$ | D. | $\frac{{\sqrt{13}}}{2}$ |
分析 本题先根据直角三角形内切圆半径得到边长的关系,结合双曲线定义和图形的对称性,得到本题结论.
解答  解:∵PF1⊥PF2,△APF1的内切圆半径为r,
解:∵PF1⊥PF2,△APF1的内切圆半径为r,
∴|PF1|+|PA|-|AF1|=2r,
∴|PF2|+2a+|PA|-|AF1|=2r,
∴|AF2|-|AF1|=2r-4,
∵由图形的对称性知:|AF2|=|AF1|,
∴r=2.
故选:A.
点评 本题考查了双曲线的定义、图形的对称性,本题难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.数列{(-1)n(2n-1)}的前2 016项和S2016等于( )
| A. | -2 016 | B. | 2 016 | C. | -2 015 | D. | 2 015 |
1.计算:log29•log38=( )
| A. | 6 | B. | 8 | C. | 10 | D. | 1 |
18.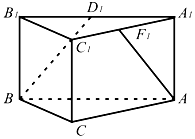 如图,直三棱柱ABC-A1B1C1中,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=2CC1,则BD1与AF1所成的角是( )
如图,直三棱柱ABC-A1B1C1中,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=2CC1,则BD1与AF1所成的角是( )
 如图,直三棱柱ABC-A1B1C1中,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=2CC1,则BD1与AF1所成的角是( )
如图,直三棱柱ABC-A1B1C1中,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=2CC1,则BD1与AF1所成的角是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
15.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线平行于直线l:3x-2y+3$\sqrt{13}$=0,且双曲线的一个焦点在直线l上,则双曲线方程为( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1 | D. | $\frac{5{x}^{2}}{16}$-$\frac{5{y}^{2}}{9}$=1 |
19.下列说法中错误的是( )
| A. | 垂直于同一条直线的两条直线相互垂直 | |
| B. | 若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行 | |
| C. | 若一个平面经过另一个平面的垂线,那么这两个平面相互垂直 | |
| D. | 若一个平面内的两条相交直线与另一个平面内的相交直线分别平行,那么这两个平面相互平行 |
 椭圆的对称中心在坐标原点,一个顶点为A(0,2),右焦点F与点$B(\sqrt{2},\sqrt{2})$的距离为2,
椭圆的对称中心在坐标原点,一个顶点为A(0,2),右焦点F与点$B(\sqrt{2},\sqrt{2})$的距离为2,