题目内容
6.数列{an}满足a1=1,且对任意的m,n∈N*都有am+n=am+an+mn,则$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{{{a_{20}}}}$等于( )| A. | $\frac{40}{21}$ | B. | $\frac{20}{21}$ | C. | $\frac{19}{10}$ | D. | $\frac{20}{19}$ |
分析 数列{an}满足a1=1,且对任意的m,n∈N*都有am+n=am+an+mn,可得an+1-an=1+n,利用“累加求和”可得an,再利用“裂项求和”即可得出.
解答 解:∵数列{an}满足a1=1,且对任意的m,n∈N*都有am+n=am+an+mn,
∴an+1-an=1+n,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=n+(n-1)+…+2+1
=$\frac{n(n+1)}{2}$.
∴$\frac{1}{{a}_{n}}$=$2(\frac{1}{n}-\frac{1}{n+1})$.
则$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{{{a_{20}}}}$=2$[(1-\frac{1}{2})$+$(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{20}-\frac{1}{21})]$=2$(1-\frac{1}{21})$=$\frac{40}{21}$.
故选:A.
点评 本题考查了等差数列的通项公式及其前n项和公式、“累加求和”与“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
4.方程lnx=$\frac{x+1}{x-1}$实数根的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
18.i是虚数单位,若复数(1-2i)(a+i)是纯虚数,且a+(b-1)i<0(a,b∈R),复数z满足|z|=3,则|z+a-bi|的最大值为( )
| A. | $3-\sqrt{5}$ | B. | $\sqrt{2}$ | C. | $3+\sqrt{5}$ | D. | $\sqrt{26}$ |
15.矩形ABCD中,AB=4,BC=2,M为AB的中点,在长方形ABCD内随机取一点P,取到的点P到M的距离大于2的概率为( )
| A. | $\frac{π}{2}$ | B. | $1-\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | $1-\frac{π}{4}$ |
16.数列{an}的前n项和为Sn,若${S_n}=3{n^2}-2n-1$,则a5=( )
| A. | 13 | B. | 25 | C. | 30 | D. | 35 |
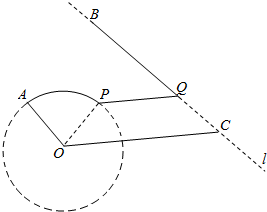 如图,B、C是海岸线l上相距50km的两个海边小城,圆O是半径为10km的某海岛小城的环岛路,A为圆O上的物资中转站,其中∠AOC=$\frac{2}{3}$π,OC=25km,且l∥OA,为使中转站A的物资运往B城,计划从A地沿环岛路至某地P,再沿水路PQ至海岸线l上Q,最后沿海岸线QB至B城修建运输线,其中PQ∥OC,Q在线段BC上.
如图,B、C是海岸线l上相距50km的两个海边小城,圆O是半径为10km的某海岛小城的环岛路,A为圆O上的物资中转站,其中∠AOC=$\frac{2}{3}$π,OC=25km,且l∥OA,为使中转站A的物资运往B城,计划从A地沿环岛路至某地P,再沿水路PQ至海岸线l上Q,最后沿海岸线QB至B城修建运输线,其中PQ∥OC,Q在线段BC上. 函数y=Asin(ωx+φ)(A>0,ω>0)的图象的一部分如图所示:
函数y=Asin(ωx+φ)(A>0,ω>0)的图象的一部分如图所示: