题目内容
4．方程lnx=$\frac{x+1}{x-1}$实数根的个数为（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 由方程的lnx-1=$\frac{2}{x-1}$，作出函数图象，通过图象的交点个数来判断方程的解的个数．
解答 解：∵lnx=$\frac{x+1}{x-1}$=1+$\frac{2}{x-1}$，∴lnx-1=$\frac{2}{x-1}$．
分别作出y=lnx-1和y=$\frac{2}{x-1}$的函数图象，
由图象可知：y=lnx-1和y=$\frac{2}{x-1}$的函数图象有两个交点，
∴方程lnx=$\frac{x+1}{x-1}$有两个实根．
故选：C．
点评 本题考查了方程根的个数判断，作出函数图象是解题关键．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
14．已知A（1，-2，11），B（6，-1，4），C（4，2，3），则△ABC为（ ）
| A． | 锐角三角形 | B． | 等腰三角形 | C． | 直角三角形 | D． | 钝角三角形 |
19．
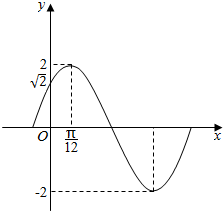已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示．则该函数的周期为（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示．则该函数的周期为（ ）| A． | $\frac{2}{3}$π | B． | $\frac{3}{4}$π | C． | $\frac{5}{6}$π | D． | π |
6．数列{an}满足a1=1，且对任意的m，n∈N*都有am+n=am+an+mn，则$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{{{a_{20}}}}$等于（ ）
| A． | $\frac{40}{21}$ | B． | $\frac{20}{21}$ | C． | $\frac{19}{10}$ | D． | $\frac{20}{19}$ |
3．“若a≠0或b≠0，则ab≠0”的否命题为（ ）
| A． | 若a≠0或b≠0，则ab=0 | B． | 若a≠0且b≠0，则ab=0 | ||
| C． | 若a=0或b=0，则ab=0 | D． | 若a=0且b=0，则ab=0 |