题目内容
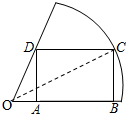
15.矩形ABCD中,AB=4,BC=2,M为AB的中点,在长方形ABCD内随机取一点P,取到的点P到M的距离大于2的概率为( )| A. | $\frac{π}{2}$ | B. | $1-\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | $1-\frac{π}{4}$ |
分析 根据几何概型的概率公式,利用数形结合进行求解即可.
解答  解:若取到的点P到M的距离大于2,则P位于阴影部分,
解:若取到的点P到M的距离大于2,则P位于阴影部分,
则矩形的面积S=4×2=8,半圆的面积S=$\frac{1}{2}×π×{2}^{2}$=2π,
则阴影部分的面积S=8-2π,
则对应的概率P=$\frac{8-2π}{8}$=$1-\frac{π}{4}$,
故选:D
点评 本题主要考查几何概型的概率计算,根据条件求出对应的区域面积是解决本题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
6.数列{an}满足a1=1,且对任意的m,n∈N*都有am+n=am+an+mn,则$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{{{a_{20}}}}$等于( )
| A. | $\frac{40}{21}$ | B. | $\frac{20}{21}$ | C. | $\frac{19}{10}$ | D. | $\frac{20}{19}$ |
3.“若a≠0或b≠0,则ab≠0”的否命题为( )
| A. | 若a≠0或b≠0,则ab=0 | B. | 若a≠0且b≠0,则ab=0 | ||
| C. | 若a=0或b=0,则ab=0 | D. | 若a=0且b=0,则ab=0 |
10.下列三句话按三段论的模式排列顺序正确的是( )
①Z1,Z2不能比较大小;②Z1,Z2是虚数;③虚数不能比较大小.
①Z1,Z2不能比较大小;②Z1,Z2是虚数;③虚数不能比较大小.
| A. | ①②③ | B. | ②①③ | C. | ②③① | D. | ③②① |
4.函数f(x)满足f(x)=$\left\{\begin{array}{l}{lo{g}_{2}(3-x),x≤0}\\{f(x-2),x>0}\end{array}\right.$,则f(3)的值为 ( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
5.正四面体的四个面上分别写有数字0,1,2,3,把两个这样的四面体抛在桌面上,露在外面的6个数字为2,0,1,3,0,3的概率为( )
| A. | $\frac{1}{9}$ | B. | $\frac{1}{64}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{16}$ |