题目内容
1.求下列函数的定义域:(1)y=$\sqrt{2cosx-1}$;
(2)y=lg(3-4sin2x)
分析 (1)y=$\sqrt{2cosx-1}$的定义域满足2cosx-1≥0,由此利用弦函数性质能求出结果.
(2)y=lg(3-4sin2x)的定义域满足3-4sin2x>0,由此利用正弦函数性质能求出结果.
解答 解:(1)y=$\sqrt{2cosx-1}$的定义域满足:
2cosx-1≥0,解得cosx$≥\frac{1}{2}$,
解得2kπ-$\frac{π}{3}$≤x$≤\frac{π}{3}$+2kπ.k∈Z.
∴y=$\sqrt{2cosx-1}$的定义域是{x|2kπ-$\frac{π}{3}$≤x$≤\frac{π}{3}$+2kπ,k∈Z}
(2)y=lg(3-4sin2x)的定义域满足:3-4sin2x>0,
解得-$\frac{\sqrt{3}}{2}≤sinx≤\frac{\sqrt{3}}{2}$,
解得-$\frac{π}{3}+2kπ≤x≤\frac{π}{3}+2kπ$,或2kπ+$\frac{2π}{3}$≤x≤2kπ+$\frac{4π}{3}$,k∈Z,
∴y=lg(3-4sin2x)的定义域为:{x|-$\frac{π}{3}+kπ≤x≤\frac{π}{3}+kπ$,k∈Z}.
点评 本题考查函数的定义域的地求法,是基础题,解题时要认真审题,注意三角函数性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.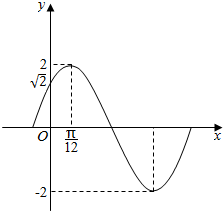 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.则该函数的周期为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.则该函数的周期为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.则该函数的周期为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.则该函数的周期为( )| A. | $\frac{2}{3}$π | B. | $\frac{3}{4}$π | C. | $\frac{5}{6}$π | D. | π |
6.已知a=logπe,b=($\sqrt{6}$)-2,c=$\frac{1}{ln2}$,则a,b,c的大小关系为( )
| A. | c>b>a | B. | c>a>b | C. | a>b>c | D. | a>c>b |
6.数列{an}满足a1=1,且对任意的m,n∈N*都有am+n=am+an+mn,则$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{{{a_{20}}}}$等于( )
| A. | $\frac{40}{21}$ | B. | $\frac{20}{21}$ | C. | $\frac{19}{10}$ | D. | $\frac{20}{19}$ |
13.已知等差数列{an}的前n项和为Sn,且a1>0,若存在正整数m≥6,使得am=Sm,当n>m时,Sn与an的大小关系是( )
| A. | Sn>an | B. | Sn=an | C. | Sn<an | D. | 不能确定 |
10.下列三句话按三段论的模式排列顺序正确的是( )
①Z1,Z2不能比较大小;②Z1,Z2是虚数;③虚数不能比较大小.
①Z1,Z2不能比较大小;②Z1,Z2是虚数;③虚数不能比较大小.
| A. | ①②③ | B. | ②①③ | C. | ②③① | D. | ③②① |
11.已知集合A={x|x≥2},B={x|1≤x≤3},则A∩B=( )
| A. | {x|-1<x≤3} | B. | {x|2≤x≤3} | C. | {x|x=3} | D. | ∅ |