题目内容
18．i是虚数单位，若复数（1-2i）（a+i）是纯虚数，且a+（b-1）i＜0（a，b∈R），复数z满足|z|=3，则|z+a-bi|的最大值为（ ）| A． | $3-\sqrt{5}$ | B． | $\sqrt{2}$ | C． | $3+\sqrt{5}$ | D． | $\sqrt{26}$ |
分析 由题意求出a，b的值，然后数形结合求得答案．
解答 
解：∵（1-2i）（a+i）=（a+2）+（1-2a）i为纯虚数，
∴a=-2，
又a+（b-1）i＜0（a，b∈R），
∴b=1，
则-a+bi=2+i，
|z+a-bi|=|z-（2+i）|，
又|z|=3，
如图：
∴|z+a-bi|的最大值为3+$\sqrt{5}$．
故选：C．
点评 本题考查复数代数形式的乘除运算，考查了复数模的求法，训练了数形结合的解题思想方法，是基础题．
练习册系列答案
相关题目
19．
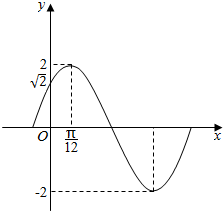已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示．则该函数的周期为（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示．则该函数的周期为（ ）| A． | $\frac{2}{3}$π | B． | $\frac{3}{4}$π | C． | $\frac{5}{6}$π | D． | π |
6．数列{an}满足a1=1，且对任意的m，n∈N*都有am+n=am+an+mn，则$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{{{a_{20}}}}$等于（ ）
| A． | $\frac{40}{21}$ | B． | $\frac{20}{21}$ | C． | $\frac{19}{10}$ | D． | $\frac{20}{19}$ |
13．已知等差数列{an}的前n项和为Sn，且a1＞0，若存在正整数m≥6，使得am=Sm，当n＞m时，Sn与an的大小关系是（ ）
| A． | Sn＞an | B． | Sn=an | C． | Sn＜an | D． | 不能确定 |
3．“若a≠0或b≠0，则ab≠0”的否命题为（ ）
| A． | 若a≠0或b≠0，则ab=0 | B． | 若a≠0且b≠0，则ab=0 | ||
| C． | 若a=0或b=0，则ab=0 | D． | 若a=0且b=0，则ab=0 |
10．下列三句话按三段论的模式排列顺序正确的是（ ）
①Z1，Z2不能比较大小；②Z1，Z2是虚数；③虚数不能比较大小．
①Z1，Z2不能比较大小；②Z1，Z2是虚数；③虚数不能比较大小．
| A． | ①②③ | B． | ②①③ | C． | ②③① | D． | ③②① |