题目内容
已知正四面体A-BCD棱长都为
,M为AC中点,N为CD中点,求异面直线BM与AN所成角的余弦值( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:异面直线及其所成的角
专题:空间角
分析:取CN中点P,连结MP,BP,BN,由MP∥AN,知∠BMP是异面直线BM与AN所成角,由此能求出异面直线BM与AN所成角的余弦值.
解答:
解:如图,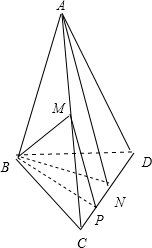 正四面体A-BCD棱长都为
正四面体A-BCD棱长都为
,M为AC中点,N为CD中点,
取CN中点P,连结MP,BP,BN,
则MP∥AN,∴∠BMP是异面直线BM与AN所成角,
由题意知BM=BN=AN=
,MP=
AN=
,
BP=
=
,
∴cos∠BMP=
=
.
∴异面直线BM与AN所成角的余弦值为
.
故选:A.
 正四面体A-BCD棱长都为
正四面体A-BCD棱长都为| 2 |
取CN中点P,连结MP,BP,BN,
则MP∥AN,∴∠BMP是异面直线BM与AN所成角,
由题意知BM=BN=AN=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
BP=
(
|
| ||
| 4 |
∴cos∠BMP=
(
| ||||||||||||
2×
|
| 1 |
| 6 |
∴异面直线BM与AN所成角的余弦值为
| 1 |
| 6 |
故选:A.
点评:本题考查异异面直线所成角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
不等式
≤0的实数解为( )
| x-20 |
| x+16 |
| A、-20≤x≤16 |
| B、-16≤x≤20 |
| C、-16<x≤20 |
| D、x<-16或x≥20 |
m∈R,复数(2m2-3m-2)+(m2-3m+2)i表示纯虚数的充要条件是( )
A、m=-
| ||
| B、m=2 | ||
C、m=-
| ||
| D、m=2或m=1 |
已知扇形的弧长为l,半径为r.类比三角形的面积公式:S=
底×高,可推知扇形的面积公式S扇形等于( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
| D、lr |
已知实数a,b满足a>b,则下列说法一定正确的是( )
| A、a-c>b-c | ||||
| B、a2>b2 | ||||
C、
| ||||
| D、ac2>bc2 |
数列{an}的通项公式为an=n2+1,则a5的值为( )
| A、5 | B、10 | C、17 | D、26 |
设△ABC的三个内角A,B,C所对的边分别是a,b,c,已知A=60°,a=
,c=
,则b=( )
| 6 |
| 2 |
A、
| ||||
B、
| ||||
C、2
| ||||
| D、3 |
在△ABC中,a=5,b=6,c=7,则
•
=( )
| AB |
| BC |
| A、19 | B、-19 |
| C、-14 | D、14 |
下列函数是奇函数的是( )
| A、f(x)=-|x| |
| B、f(x)=2x+2-x |
| C、f(x)=lg(1+x)-lg(1-x) |
| D、f(x)=x3-1 |