题目内容
16.设函数f(x)=|x-1|+|x-3|.(1)解不等式:f(x)≤4;
(2)对?x∈R,a2-|a|≤f(x),求实数a的取值范围.
分析 (1)利用零点法,去除绝对值符号,解相应的不等式,最后综合讨论结果,可得答案;
(2)先利用绝对值三角不等式求f(x)的最小值,进而利用零点分段法,可得实数a的取值范围.
解答 解:(1)当x<1时,不等式f(x)≤4可化为:4-2x≤4,解得:x≥0,
∴0≤x<1;
当1≤x≤3时,不等式f(x)≤4可化为:2≤4,恒成立;
当x>3时,不等式f(x)≤4可化为:2x-4≤4,解得:x≤4,
∴3<x≤4,
综上可得:原不等式的解集为:[0,4];
(2)∵f(x)=|x-1|+|x-3|=|1-x|+|x-3|≥|1-x+x-3|=2.
若对?x∈R,a2-|a|≤f(x),
则a2-|a|≤2,
当a≥0时,即a2-a-2≤0,解得:-1≤a≤2,
∴0≤a≤2,
当a<0时,即a2+a-2≤0,解得:-2≤a≤1,
∴-2≤a<0,
综上可得实数a的取值范围为:[-2,2].
点评 本题考查的知识点是绝对值不等式的解法,绝对值三角不等式,零点分段法,难度中档.

练习册系列答案
相关题目
6.在等腰三角形ABC中,过直角顶点C在∠ACB内作一条射线CD与线段AB交于点D,则AD<AC的概率是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{{2-\sqrt{2}}}{2}$ | D. | $\frac{3}{4}$ |
7.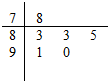 对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶如图所示,给出关于该同学数学成绩的以下说法:
对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶如图所示,给出关于该同学数学成绩的以下说法:
①中位数为83;②众数为83;③平均数为85;④极差为12.
其中正确说法序号是( )
 对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶如图所示,给出关于该同学数学成绩的以下说法:
对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶如图所示,给出关于该同学数学成绩的以下说法:①中位数为83;②众数为83;③平均数为85;④极差为12.
其中正确说法序号是( )
| A. | ①② | B. | ③④ | C. | ②③ | D. | ①③ |
4.设直线y=3x-2与椭圆Г:$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1交于A,B两点,过A,B两点的圆与椭圆Г交于另外两点C,D,则直线CD的斜率k为( )
| A. | -$\frac{1}{3}$ | B. | -3 | C. | $\frac{1}{2}$ | D. | -2 |
8.已知离心率为e的椭圆Γ:$\frac{{x}^{2}}{{a}^{2}-4}$+$\frac{{y}^{2}}{{a}^{2}}$=1(a>2)的上、下焦点分别为F1和F2,过点(0,2)且不与y轴垂直的直线与椭圆交于M,N两点,若△MNF2为等腰直角三角形,则e=( )
| A. | $\sqrt{3}$-$\sqrt{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{6}$$-\sqrt{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
5.设a=e${\;}^{-\sqrt{2}}$,b=log0.29,c=lnπ(e为自然对数的底数),则a,b,c的大小关系为( )
| A. | b<a<c | B. | b<c<a | C. | a<b<c | D. | c<b<a |