题目内容
6.已知实数x、y满足$\left\{\begin{array}{l}{x-y-1≤0}\\{2x-y-3≥0}\end{array}\right.$,在区间(0,5)内任取两数a、b.则目标函数z=ax+by的最小值大于2$\sqrt{5}$的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 作出不等式组对应的平面区域,利用线性规划的知识求出z=ax+by的最小值,然后根据几何概型的概率公式进行求解即可.
解答 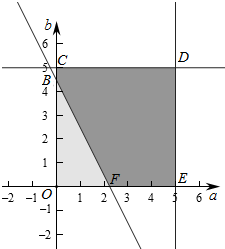
 解:由z=ax+by(a>0,b>0)得$y=-\frac{a}{b}x+\frac{z}{b}$,
解:由z=ax+by(a>0,b>0)得$y=-\frac{a}{b}x+\frac{z}{b}$,
∵0<a<5,0<b<5,∴直线的斜率$-\frac{a}{b}<0$,
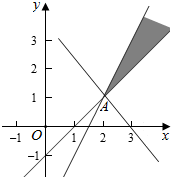
作出不等式对应的平面区域如图:
平移直线得$y=-\frac{a}{b}x+\frac{z}{b}$,由图象可知当直线$y=-\frac{a}{b}x+\frac{z}{b}$经过点A时,直线$y=-\frac{a}{b}x+\frac{z}{b}$的截距最小,此时z最最小.
由$\left\{\begin{array}{l}{x-y-1=0}\\{2x-y-3=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,即A(2,1),即z的最小值为z=2a+b,
若2a+b>2$\sqrt{5}$,
∵$\left\{\begin{array}{l}{0<a<5}\\{0<b<5}\end{array}\right.$,∴作出不等式组对应的平面区域如图:
则2a+b>2$\sqrt{5}$对应的区域为五边形BCDEF,
则正方形OCDE的面积S=5×5=25,
当a=0时,由2a+b=2$\sqrt{5}$,得b=2$\sqrt{5}$,即B(0,2$\sqrt{5}$),
当b=0时,由2a+b=2$\sqrt{5}$,得a=$\sqrt{5}$,即B($\sqrt{5}$,0),
则△OBF的面积S=$\frac{1}{2}×$2$\sqrt{5}$×$\sqrt{5}$=5,
则五边形BCDEF的面积S=25-5=20,
则对应的概率P=$\frac{20}{25}$=$\frac{4}{5}$,
故选:D.
点评 本题主要考查线性规划以及几何概型的概率的计算,作出不等式组对应的平面区域求出目标函数的最小值是解决本题的关键.

| A. | (-2,-1) | B. | (-1,0) | C. | (1,2) | D. | (0,1) |
| A. | (4,+∞) | B. | (-∞,0] | C. | [4,+∞) | D. | (-∞,0) |