题目内容
已知集合M={(x,y)|x+y≤8,x≥0,y≥0},N={(x,y)|x-3y≥0,x≤6,y≥0},若向区域M内随机投一点,则点P落入区域N的概率为 .
考点:几何概型
专题:计算题,概率与统计
分析:我们分别作出集合M所表示的平面区域,即满足条件x+y≤8,x≥0,y≥0的可行域,并求出其面积用来表示全部基本事件,再求出N所表示的平面区域,即满足条件x-3y≥0,x≤6,y≥0的可行域,并求出其面积,代入几何概型公式,即可求解.
解答:
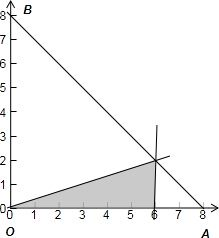 解:满足条件M={(x,y)|x+y≤8,x≥0,y≥0}的平面区域如下图中△OAB所示:其中满足条件N={(x,y)|x-3y≥0,x≤6,y≥0}的平面区域如图中阴影部分所示,
解:满足条件M={(x,y)|x+y≤8,x≥0,y≥0}的平面区域如下图中△OAB所示:其中满足条件N={(x,y)|x-3y≥0,x≤6,y≥0}的平面区域如图中阴影部分所示,
则向区域M内随机投一点P,则点P落入区域N内的概率
P=
=
=
.
故答案为:
.
 解:满足条件M={(x,y)|x+y≤8,x≥0,y≥0}的平面区域如下图中△OAB所示:其中满足条件N={(x,y)|x-3y≥0,x≤6,y≥0}的平面区域如图中阴影部分所示,
解:满足条件M={(x,y)|x+y≤8,x≥0,y≥0}的平面区域如下图中△OAB所示:其中满足条件N={(x,y)|x-3y≥0,x≤6,y≥0}的平面区域如图中阴影部分所示,则向区域M内随机投一点P,则点P落入区域N内的概率
P=
| S阴影 |
| S△OAB |
| ||
|
| 3 |
| 16 |
故答案为:
| 3 |
| 16 |
点评:本题考查的知识点是几何概型,几何概型解题步骤为:求出满足条件A的基本事件对应的平面区域面积N(A),再求出总的基本事件对应平面区域面积N,最后根据P=
求解.
| N(A) |
| N |

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
数列{an}满足a0=
,an+1=[an]+
,([an]与{an}分别表示an的整数部分与分数部分),则a2014=( )
| 3 |
| 1 |
| {an} |
A、3020+
| ||||
B、3020+
| ||||
C、
| ||||
D、3018+
|
函数f(x)=xlnx在x=1处的切线为( )
| A、y=x+1 |
| B、y=x-1 |
| C、y=1-x |
| D、y=1-2x |