题目内容
设集合M=[0,1),N=[1,2),函数f(x)=
.
(1)若x∈M,g(x)=f2(x)-2f(x)+a,且g(x)的最小值为1,求实数a的值;
(2)若x0∈M,且f(f(x0))∈M,求x0的取值范围.
|
(1)若x∈M,g(x)=f2(x)-2f(x)+a,且g(x)的最小值为1,求实数a的值;
(2)若x0∈M,且f(f(x0))∈M,求x0的取值范围.
考点:二次函数在闭区间上的最值,函数的值域
专题:函数的性质及应用
分析:(1)若x∈M,令t=2x,则y=(t-1)2+a-1,且t∈[1,2),再利用二次函数的性质求得函数的最小值,再根据函数的最小值为1,求得a的值.
(2)当x∈M,f(x)∈[1,2);当x∈N,f(x)∈[0,2],令t=f(x0),则f(t)∈M,即0≤f(t)≤1,求得t的范围,可得f(x0)的范围,从而求得x0的取值范围.
(2)当x∈M,f(x)∈[1,2);当x∈N,f(x)∈[0,2],令t=f(x0),则f(t)∈M,即0≤f(t)≤1,求得t的范围,可得f(x0)的范围,从而求得x0的取值范围.
解答:
解:(1)若x∈M,令t=2x,则y=t2-2t+a=(t-1)2+a-1,且t∈[1,2),
故当t=1时,函数取得最小为a-1=1,∴a=2.
(2)当x∈M,f(x)=2x∈[1,2);当x∈N,f(x)=4-2x∈[0,2],
令t=f(x0),∴f(t)∈M.
∵0≤f(t)≤1,∴0≤4-2t<1,∴
<t<3,
∴
<f(x0)<α,∴
<2x0<2,∴log2
<x0<1,即x0的取值范围为(log2
,1).
故当t=1时,函数取得最小为a-1=1,∴a=2.
(2)当x∈M,f(x)=2x∈[1,2);当x∈N,f(x)=4-2x∈[0,2],
令t=f(x0),∴f(t)∈M.
∵0≤f(t)≤1,∴0≤4-2t<1,∴
| 3 |
| 2 |
∴
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题主要考查求二次函数在闭区间上的最值,求函数的值域,注意换元过程中变量范围的改变,属于中档题.

练习册系列答案
相关题目
下列函数中,既是偶函数又在(0,+∞)单调递增的函数是( )
| A、y=3x | ||
| B、y=|x|+1 | ||
| C、y=-x2+1 | ||
D、y=
|
已知扇形的面积等于
cm2,弧长为
cm,则圆心角等于( )
| π |
| 6 |
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在区间(-∞,0)上为增函数的是( )
| A、y=1 | ||
| B、y=1+x2 | ||
| C、y=-x2-2x-1 | ||
D、y=
|
已知实数a,b满足(
)a>(
)b,则下列不等式一定成立的是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、a2>b2 |
| B、|a|<|b| |
| C、log2a<log2b |
| D、1-2a>1-2b |
 一个几何体的三视图如图所示(单位:m),则该几何体的体积为( )
一个几何体的三视图如图所示(单位:m),则该几何体的体积为( )| A、9+π | B、6+π |
| C、6+3π | D、9+3π |
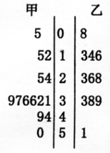 如图为甲、乙两名篮球运动员每场比赛的得分情况的茎叶图,则甲运动员的得分的中位数是
如图为甲、乙两名篮球运动员每场比赛的得分情况的茎叶图,则甲运动员的得分的中位数是