题目内容
在区间(-∞,0)上为增函数的是( )
| A、y=1 | ||
| B、y=1+x2 | ||
| C、y=-x2-2x-1 | ||
D、y=
|
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:根据基本函数的单调性逐项判断即可得到答案.
解答:
解:A中,y=1在(-∞,0)上不单调,故排除A;
B中,y=1+x2在(-∞,0)上单调递减,故排除B;
C中,y=-x2-2x-1在(-∞,-1)上递增,在(-1,+∞)上递减,故y=-x2-2x-1在(-∞,0)上不单调,排除C;
D中,y=
=
=1-
在(-∞,1)上递增,在(1,+∞)上递增,故y=
在(-∞,0)上为增函数,
故选D.
B中,y=1+x2在(-∞,0)上单调递减,故排除B;
C中,y=-x2-2x-1在(-∞,-1)上递增,在(-1,+∞)上递减,故y=-x2-2x-1在(-∞,0)上不单调,排除C;
D中,y=
| 2-x |
| 1-x |
| x-2 |
| x-1 |
| 1 |
| x-1 |
| 2-x |
| 1-x |
故选D.
点评:本题考查函数单调性的判断,属基础题,熟记基本函数的单调性是解决问题的基础.

练习册系列答案
相关题目
设a=50.3,b=0.35,c=log50.3+log52,则a,b,c的大小关系是( )
| A、b<c<a |
| B、a<b<c |
| C、c<a<b |
| D、c<b<a |
过椭圆C:
+
=1上任一点P,作椭圆C的右准线的垂线PH(H为垂足),延长PH到点Q,使|HQ|=λ|PH|(λ≥1).当点P在椭圆C上运动时,点Q的轨迹的离心率的取值范围为( )
| x2 |
| 3 |
| y2 |
| 2 |
A、(0,
| ||||||||
B、(
| ||||||||
C、[
| ||||||||
D、(
|
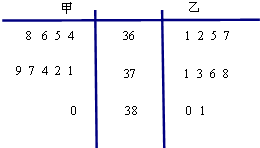 学校为了预防甲流感,每天上午都要对同学进行体温抽查.某一天,随机抽取甲、乙两个班级各10名同学,测量他们的体温如图:(单位0.1℃)
学校为了预防甲流感,每天上午都要对同学进行体温抽查.某一天,随机抽取甲、乙两个班级各10名同学,测量他们的体温如图:(单位0.1℃)