题目内容
不全相等的五个数a、b、c、m、n具有关系如下:a、b、c成等比数列,a、m、b和b、n、c都成等差数列,则
+
=( )
| a |
| m |
| c |
| n |
| A、-2 | B、0 | C、2 | D、不能确定 |
考点:等比数列的通项公式,等差数列的通项公式
专题:等差数列与等比数列
分析:由已知得2m=a+b,2n=b+c,b2=ac,从而
+
=
=
=
=2.
| a |
| m |
| c |
| n |
| an+cm |
| mn |
| 2(ab+ac+ac+bc) |
| (a+b)(b+c) |
| 2(ab+2b2+bc) |
| ab+2b2+bc |
解答:
解:由已知得2m=a+b,2n=b+c,b2=ac,
∴
+
=
=
[
+
]
=
=
=2.
故选:C.
∴
| a |
| m |
| c |
| n |
| an+cm |
| mn |
=
| 1 |
| mn |
| a(b+c) |
| 2 |
| c(a+b) |
| 2 |
=
| 2(ab+ac+ac+bc) |
| (a+b)(b+c) |
=
| 2(ab+2b2+bc) |
| ab+2b2+bc |
故选:C.
点评:本题考查代数和的求法,是基础题,解题时要认真审题,注意等差数列和等比数列的性质的合理运用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
某几何体的三视图如图,若该几何体的所有顶点都在一个球面上,则该球面的表面积为( )


| A、4π | ||
B、
| ||
C、
| ||
| D、20π |
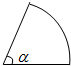 现要用篱笆围成一个面积为S扇形菜园(如图所示),问要使这个菜园所用篱笆最短,则这个扇形的半径和圆心角各为( )
现要用篱笆围成一个面积为S扇形菜园(如图所示),问要使这个菜园所用篱笆最短,则这个扇形的半径和圆心角各为( )A、
| ||
B、2
| ||
C、
| ||
D、2
|
若复数z满足z(2+i)=5i-10,则|z|=( )
| A、25 | ||
B、5
| ||
C、
| ||
| D、5 |
已知点M(2,-3),N(-3,-2),直线ax+y-1-a=0与线段MN相交,则实数a的取值范围是( )
A、-
| ||
B、-4≤a≤
| ||
C、a≤-
| ||
D、a≤-4或a≥
|
函数f(x)=
的定义域为R,则实数a的取值范围是( )
| 1 |
| ax2+4ax+3 |
A、[0,
| ||
B、(0,
| ||
C、(
| ||
| D、(-∞,0) |
 在平面向量中有如下定理:设点O、P、Q、R为同一平面内的点,则P、Q、R三点共线的充要条件是:存在实数t,使
在平面向量中有如下定理:设点O、P、Q、R为同一平面内的点,则P、Q、R三点共线的充要条件是:存在实数t,使 函数f(x)=2sin(ωx+φ)(ω>0,
函数f(x)=2sin(ωx+φ)(ω>0,