题目内容
直线l:y=x+b与抛物线C:x2=4y相切于点A.
(Ⅰ) 求实数b的值,及点A的坐标;
(Ⅱ) 求过点B(0,-1)的抛物线C的切线方程.
(Ⅰ) 求实数b的值,及点A的坐标;
(Ⅱ) 求过点B(0,-1)的抛物线C的切线方程.
考点:抛物线的应用
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)直线l:y=x+b与抛物线C:x2=4y联立,消去y,利用直线l与抛物线C相切,可得△=(-4)2-4×(-4b)=0,即可求实数b的值,及点A的坐标;
(Ⅱ)设过点B(0,-1)的抛物线C的切线方程为y=kx-1,与抛物线C:x2=4y联立,消去y,利用直线l与抛物线C相切,可得△=0.即可求出过点B(0,-1)的抛物线C的切线方程.
(Ⅱ)设过点B(0,-1)的抛物线C的切线方程为y=kx-1,与抛物线C:x2=4y联立,消去y,利用直线l与抛物线C相切,可得△=0.即可求出过点B(0,-1)的抛物线C的切线方程.
解答:
解:(Ⅰ)直线l:y=x+b与抛物线C:x2=4y联立,消去y,可得x2-4x-4b=0. (*)
因为直线l与抛物线C相切,所以△=(-4)2-4×(-4b)=0,解得b=-1;
代入方程(*)即为x2-4x+4=0,解得x=2,y=1,故点A(2,1).
(Ⅱ)设过点B(0,-1)的抛物线C的切线方程为y=kx-1.
与抛物线C:x2=4y联立,消去y,可得x2-4kx+4=0,
因为直线l与抛物线C相切,所以△=(-4k)2-4×4=0,解得k=±1,
所以过点B(0,-1)的抛物线C的切线方程为y=±x-1.
因为直线l与抛物线C相切,所以△=(-4)2-4×(-4b)=0,解得b=-1;
代入方程(*)即为x2-4x+4=0,解得x=2,y=1,故点A(2,1).
(Ⅱ)设过点B(0,-1)的抛物线C的切线方程为y=kx-1.
与抛物线C:x2=4y联立,消去y,可得x2-4kx+4=0,
因为直线l与抛物线C相切,所以△=(-4k)2-4×4=0,解得k=±1,
所以过点B(0,-1)的抛物线C的切线方程为y=±x-1.
点评:本题考查直线与抛物线的位置关系,考查学生的计算能力,正确联立直线与抛物线方程是关键.

练习册系列答案
相关题目
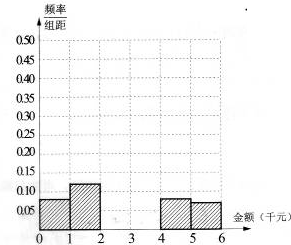 某网络营销部门随机抽查了某市200名网友在2013年11月11日的网购金额,所得数据如下表:
某网络营销部门随机抽查了某市200名网友在2013年11月11日的网购金额,所得数据如下表: