题目内容
已知函数f(x)=mx2+3(m-4)x-9,m为常数
(1)判断函数f(x)是否存在零点,若存在指出存在几个;
(2)若函数f(x)存在两个零点x1,x2,试确定实数m的值,使两个零点间的距离最小,并求出这个最小距离;
(3)设m>0,当x∈[-3,-
]时,f(x)的值域为{y|0≤y≤27},求m的值.
(1)判断函数f(x)是否存在零点,若存在指出存在几个;
(2)若函数f(x)存在两个零点x1,x2,试确定实数m的值,使两个零点间的距离最小,并求出这个最小距离;
(3)设m>0,当x∈[-3,-
| 3 |
| 2 |
考点:根的存在性及根的个数判断,函数的值域
专题:函数的性质及应用
分析:(1)分别讨论m=0和m≠0两种情况,利用一次函数和二次函数的零点判断方法分别判断零点个数;
(2)利用韦达定理,将d=|x1-x2|转化为关于m的函数,利用配方法求最值即可;
(3)若x∈[-3,-
]时,f(x)的值域为{y|0≤y≤27},则f(x)在[-3,-
]单调,由f(-3)=27,可得:f(-
)=0,进而得到m的值.
(2)利用韦达定理,将d=|x1-x2|转化为关于m的函数,利用配方法求最值即可;
(3)若x∈[-3,-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:(1)当m=0时,f(x)=-12x-9,函数的零点为x=-
,即函数只有一个零点.
当m≠0时,△=9(m-4)2+36m=(m-2)2+12>0,
∴函数f(x)的零点的个数为2.
故当m=0时,函数f(x)的零点的个数为1;当m≠0时,函数f(x)的零点的个数为2;
(2)若函数f(x)有两个零点x1,x2,则m≠0,
x1+x2=
,x1•x2=
,
∴d=|x1-x2|=
=
=12
≥12×
=
(m=8时取等号),
∴d=|x1-x2|的最小值为
;
(3)若x∈[-3,-
]时,f(x)的值域为{y|0≤y≤27},
则f(x)在[-3,-
]单调,
∵f(-3)=27,
∴f(-
)=0
即-
m+9=0,解得m=4
| 3 |
| 4 |
当m≠0时,△=9(m-4)2+36m=(m-2)2+12>0,
∴函数f(x)的零点的个数为2.
故当m=0时,函数f(x)的零点的个数为1;当m≠0时,函数f(x)的零点的个数为2;
(2)若函数f(x)有两个零点x1,x2,则m≠0,
x1+x2=
| 12-3m |
| m |
| -9 |
| m |
∴d=|x1-x2|=
| (x1+x2)2-4x1•x2 |
(
|
(m-
|
|
3
| ||
| 2 |
∴d=|x1-x2|的最小值为
3
| ||
| 2 |
(3)若x∈[-3,-
| 3 |
| 2 |
则f(x)在[-3,-
| 3 |
| 2 |
∵f(-3)=27,
∴f(-
| 3 |
| 2 |
即-
| 9 |
| 4 |
点评:本题考查了二次函数零点判断方法,二次方程根与系数关系的应用,不等式恒成立问题的解法及配方法求二次函数的最值,考查了数学转化思想方法,是中档题.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
已知a>1,在约束条件
下,目标函数z=x+ay的最大值小于2,则a的取值范围是( )
|
| A、(1,3) | ||
| B、(3,+∞) | ||
C、(
| ||
D、(1,
|

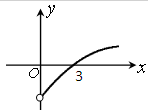 已知f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,当x>0时,y=f(x)的图象如图所示,解不等式xf(x)<0.
已知f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,当x>0时,y=f(x)的图象如图所示,解不等式xf(x)<0.