题目内容
19．若函数y=cos2x-3cosx+a的最小值是-$\frac{3}{2}$，求a的值．分析 利用配方法变形，然后利用二次函数的单调性求出函数的最值，结合函数y=cos2x-3cosx+a的最小值是-$\frac{3}{2}$，求得a的取值．
解答 解：y=cos2x-3cosx+a=$（cosx-\frac{3}{2}）^{2}-\frac{9}{4}+a$，
∵-1≤cosx≤1，
∴函数在[-1，1]上单调递减，
${y}_{min}=（1-\frac{3}{2}）^{2}-\frac{9}{4}+a=-\frac{3}{2}$，
∴a=$\frac{1}{2}$．
点评 本题考查函数的最值，训练了配方法求函数的最值，属于基础题．
练习册系列答案
计算高手系列答案
相关题目
9．
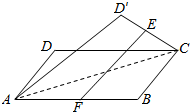设E，F分别是正方形ABCD中CD、AB边的中点，将△ADC沿对角线AC对折，使得直线EF与AC异面，记直线EF与平面ABC所成角为α，与异面直线AC所成角为β，则当tanβ=$\frac{1}{2}$时，tanα=（ ）
设E，F分别是正方形ABCD中CD、AB边的中点，将△ADC沿对角线AC对折，使得直线EF与AC异面，记直线EF与平面ABC所成角为α，与异面直线AC所成角为β，则当tanβ=$\frac{1}{2}$时，tanα=（ ）| A． | $\frac{3\sqrt{5}}{16}$ | B． | $\frac{\sqrt{5}}{5}$ | C． | $\frac{\sqrt{51}}{17}$ | D． | $\frac{\sqrt{57}}{19}$ |
10．在梯形ABCD中，AB∥CD，$\overrightarrow{AB}$=2$\overrightarrow{DC}$，$\overrightarrow{BE}$=$\overrightarrow{EC}$，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，则向量$\overrightarrow{AE}$等于（ ）
| A． | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | B． | $\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | C． | $\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ | D． | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ |
8．已知a2≤1，|b|≤1，则满足函数y=log3（x2+2ax+b）的定义域为全体实数R的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |