题目内容

10．设等差数列{an}的前n项和为Sn，若S6=9，S12=36，则a13+a14+…+a18=（　　）
A．63B．45C．36D．27

分析 由等差数列的性质得S6，S12-S6，S18-S12成等差数列，由此能求出a13+a14+…+a18的值．

解答 解：∵等差数列{an}的前n项和为Sn，S6=9，S12=36，
S6，S12-S6，S18-S12成等差数列，
即9，36-9=27，S18-36成等差数列，
∴2×27=9+S8-36，
S8-36=54-9=45．
∴a13+a14+…+a18=S8-36=45．
故选：B．

点评 本题考查等差数列的若干项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．

练习册系列答案
相关题目
20．已知函数f（x）=ax2-4ax+b（a＞0）在区间[0，1]上有最大值1和最小值-2．
（1）求a，b的值；
（2）若不等式f（x）≥mx在x∈（0，+∞）上恒成立，求实数m的取值范围．
1．在△ABC中，角A，B，C的对边分别为a，b，c，c=5且b（2sinB+sinA）+（2a+b）sinA=2csinC．
（1）求C的值；
（2）若cosA=$\frac{4}{5}$，求b的值．
18．直线l的方程为$|\begin{array}{l}{1}&{0}&{2}\\{x}&{2}&{3}\\{y}&{-1}&{2}\end{array}|$=0，则直线l的倾斜角为π-arctan$\frac{1}{2}$．
5．若存在两个正实数x、y，使得等式x+a（y-2ex）（lny-lnx）=0成立，其中e为自然对数的底数，则实数a的取值范围为a＜0或a≥$\frac{1}{e}$．
15．已知集合A={-2，-1，1，2，3}，B={x|1≤2x≤4}，则A∩B等于（　　）
A．{1，2，3}B．{-1，1，2}C．{0，1，2，3}D．{1，2}
2．函数y=0.75sin（x+$\frac{π}{4}$）（x∈[-π，π]）的递减区间是[-π，-$\frac{3π}{4}$]，[$\frac{π}{4}$，π]；
函数y=$\sqrt{3}$cos（$\frac{1}{2}$x+$\frac{2π}{3}$）（x∈[0，2π]）的递增区间是[$\frac{2π}{3}$，2π]；
函数y=$\frac{3}{5}$sin（3x-$\frac{π}{6}$）（x∈R）的递增区间是[-$\frac{π}{9}$+$\frac{2kπ}{3}$，$\frac{2π}{9}$+$\frac{2kπ}{3}$]，k∈Z．
19．设数列{an}满足：an+1=$\frac{1+{a}_{n}}{1-{a}_{n}}$，a2015=3，那么a1等于（　　）
A．$\frac{1}{2}$B．2C．-$\frac{1}{3}$D．3
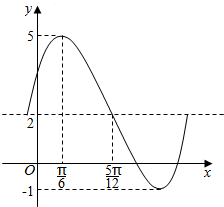20．已知函数f（x）=Asin（ωx+φ）+b（A＞0，ω＞0，0＜φ＜π，b为常数）的一段图象如图所示．
（1）求函数f（x）的解析式；
（2）函数f（x）在y轴右侧的极小值点的横坐标组成数列{an}，设右侧的第一个极小值点的横坐标为首项为a1，试求数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和Sn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网