题目内容
20.已知函数f(x)=ax2-4ax+b(a>0)在区间[0,1]上有最大值1和最小值-2.(1)求a,b的值;
(2)若不等式f(x)≥mx在x∈(0,+∞)上恒成立,求实数m的取值范围.
分析 (1)求得f(x)的对称轴方程,可得f(x)在[0,1]递减,即可得到最值,解方程可得a,b的值;
(2)由题意可得$m≤x-4+\frac{1}{x}$在x∈(0,+∞)上恒成立,运用对号函数的单调性,可得右边函数的最小值,即可得到m的范围.
解答 解:(1)函数f(x)=ax2-4ax+b(a>0)=a(x-2)2+b-4a,
∵a>0,开口向上,对称轴x=2,
∴f(x)在[0,1]递减,
∴f(0)=b=1,f(1)=b-3a=-2,
∴a=b=1;
(2)∵f(x)=x2-4x+1≥mx在x∈(0,+∞)上恒成立,
∴$m≤x-4+\frac{1}{x}$在x∈(0,+∞)上恒成立,
∵双勾函数y=x+$\frac{1}{x}$在(0,1]递减,在[1,+∞)递增,
∴当x=1时,x-4+$\frac{1}{x}$取得最小值,且为2-4=-2,
则m≤-2.
点评 本题考查二次函数的最值的求法,注意讨论对称轴和区间的关系,考查不等式恒成立问题的解法,注意运用参数分离和对号函数的单调性,考查运算能力,属于中档题.

练习册系列答案
相关题目
10.已知双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为$\sqrt{2}$,且双曲线与抛物线x2=-4$\sqrt{3}$y的准线交于A,B,S△OAB=$\sqrt{3}$,则双曲线的实轴长( )
| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 2 | D. | 4 |
11.函数$y={log_{\frac{1}{4}}}({-{x^2}+2x+3})$的单调增区间是( )
| A. | (-1,1] | B. | (-∞,1) | C. | [1,3) | D. | (1,+∞) |
15.下列式子中,不能化简为$\overrightarrow{PQ}$的是( )
| A. | $\overrightarrow{AB}+\overrightarrow{PA}+\overrightarrow{BQ}$ | B. | $\overrightarrow{AB}+\overrightarrow{PC}+\overrightarrow{BA}-\overrightarrow{QC}$ | C. | $\overrightarrow{QC}+\overrightarrow{CQ}-\overrightarrow{QP}$ | D. | $\overrightarrow{PA}+\overrightarrow{AB}-\overrightarrow{BQ}$ |
12.$\frac{3+2i}{2-3i}$=( )
| A. | 1+i | B. | 1-i | C. | i | D. | -i |
10.设等差数列{an}的前n项和为Sn,若S6=9,S12=36,则a13+a14+…+a18=( )
| A. | 63 | B. | 45 | C. | 36 | D. | 27 |
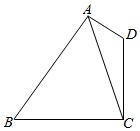 如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cosB=$\frac{\sqrt{3}}{3}$.
如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cosB=$\frac{\sqrt{3}}{3}$.