题目内容
4．已知函数$f（x）={x^2}-2xsin（\frac{π}{2}x）+1$的两个零点分别为m、n（m＜n），则$\int_m^n{\sqrt{1-{x^2}}}dx$=$\frac{π}{2}$．分析 先求出m，n，再利用几何意义求出定积分．
解答 解：∵函数$f（x）={x^2}-2xsin（\frac{π}{2}x）+1$的两个零点分别为m、n（m＜n），
∴m=-1，n=1，
∴$\int_m^n{\sqrt{1-{x^2}}}dx$=${∫}_{-1}^{1}\sqrt{1-{x}^{2}}dx$=$\frac{1}{2}π•{1}^{2}$=$\frac{π}{2}$．
故答案为$\frac{π}{2}$．
点评 本题考查函数的零点，考查定积分知识的运用，求出m，n是关键．
练习册系列答案
步步高达标卷系列答案
相关题目
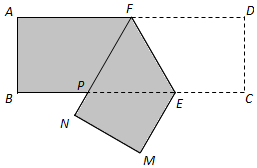如图，某机械厂要将长6m，宽2m的长方形铁皮ABCD进行裁剪．已知点F为AD的中点，点E在边BC上，裁剪时先将四边形CDFE沿直线EF翻折到MNFE处（点C，D分别落在直线BC下方点M，N处，FN交边BC于点P），再沿直线PE裁剪．
19．在正数数列{an}中，a1=2，且点$（a_n^2，a_{n-1}^2）$在直线x-9y=0上，则{an}的前n项和Sn等于（ ）
| A． | 3n-1 | B． | $\frac{{1-{{（{-3}）}^n}}}{2}$ | C． | $\frac{{1+{3^n}}}{2}$ | D． | $\frac{{3{n^2}+n}}{2}$ |