题目内容
13.已知向量$\overrightarrow a=(λ,1)$,$\overrightarrow b=(λ+2,1)$,若$|\overrightarrow a+\overrightarrow b|=|\overrightarrow a-\overrightarrow b|$,则实数λ的值为( )| A. | -1 | B. | 2 | C. | 1 | D. | -2 |
分析 根据题意,由向量模的定义,将$|\overrightarrow a+\overrightarrow b|=|\overrightarrow a-\overrightarrow b|$变形分析可得$\overrightarrow{a}$•$\overrightarrow{b}$=0,又由向量$\overrightarrow{a}$、$\overrightarrow{b}$的坐标,可得λ(λ+2)+1=0,解可得λ的值,即可得答案.
解答 解:根据题意,对于向量$\overrightarrow{a}$、$\overrightarrow{b}$,若有$|\overrightarrow a+\overrightarrow b|=|\overrightarrow a-\overrightarrow b|$,
则有|$\overrightarrow{a}$+$\overrightarrow{b}$|2=|$\overrightarrow{a}$-$\overrightarrow{b}$|2,
变形可得$\overrightarrow{a}$2+2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2=$\overrightarrow{a}$2-2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2,
即$\overrightarrow{a}$•$\overrightarrow{b}$=0,
又由向量$\overrightarrow a=(λ,1)$,$\overrightarrow b=(λ+2,1)$,
则有λ(λ+2)+1=0,
解可得λ=-1;
故选:A.
点评 本题考查向量的数量积的运算,涉及向量的坐标运算,关键掌握向量模的性质,进而分析得到$\overrightarrow{a}$、$\overrightarrow{b}$的关系.

 轻松课堂标准练系列答案
轻松课堂标准练系列答案| A. | 2和1 | B. | 2和0 | C. | 2和-1 | D. | 2和-2 |
| A. | $(-\frac{1}{e},0)∪(0,\frac{1}{e})$ | B. | $(-\frac{1}{2},0)∪(\frac{1}{2},1)$ | C. | $(-1,-\frac{1}{e})∪(\frac{1}{e},1)$ | D. | $(-1,-\frac{1}{2})∪(0,\frac{1}{2})$ |
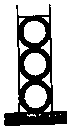 圆柱形容器内盛有高度为6cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是3cm.
圆柱形容器内盛有高度为6cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是3cm.