题目内容
函数y=
sin(x-
)得图象的一条对称轴是直线( )
| 1 |
| 2 |
| π |
| 3 |
A、x=-
| ||
B、x=
| ||
C、x=-
| ||
D、x=
|
考点:正弦函数的对称性
专题:三角函数的求值
分析:利用正弦函数的对称轴方程,再令k=-1,即可求得结论.
解答:
解:由题意,令x-
=
+kπ(k∈Z),则x=
+kπ(k∈Z),
令k=-1,则x=-
∴函数y=
sin(x-
)得图象的一条对称轴是直线x=-
.
故选C.
| π |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
令k=-1,则x=-
| π |
| 6 |
∴函数y=
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
故选C.
点评:本题考查三角函数的性质,考查学生的计算能力,属于中档题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
函数f(x)的导函数f′(x)的图象如图所示,则下列说法正确的是( )
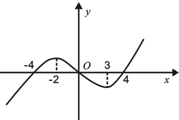

| A、函数f(x)在(-2,3)内单调递减 |
| B、函数f(x)在x=3处取极小值 |
| C、函数f(x)在(-4,0)内单调递增 |
| D、函数f(x)在x=4处取极大值 |
若函数f(x)=3x,它的反函数是g(x),a=g(3),b=g(4),c=g(π),则下面关系式中正确的是( )
| A、a<b<c |
| B、a<c<b |
| C、b<c<a |
| D、b<a<c |
命题“若a2>b2,则a>b”的否命题是( )
| A、若a2≤b2则,则a>b |
| B、若a2<b2,则a<b |
| C、若a2≤b2则,则a≤b |
| D、若a2<b2,则a>b |