题目内容
6．设f（x）=$\left\{\begin{array}{l}{2-{3}^{x-1}，x＜2}\\{lo{g}_{5}（3x-4），x≥2}\end{array}\right.$，则f（f（3））的值为1．分析 先求出∴f（3）=log5（3×3-4）=log55=1，从而f（f（3））=f（1），由此能求出结果．
解答 解：∵f（x）=$\left\{\begin{array}{l}{2-{3}^{x-1}，x＜2}\\{lo{g}_{5}（3x-4），x≥2}\end{array}\right.$，
∴f（3）=log5（3×3-4）=log55=1，
f（f（3））=f（1）=2-30=1．
故答案为：1．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
名校名卷单元同步训练测试题系列答案
相关题目
16．
随着人们经济收入的不断增长，个人购买家庭轿车已不再是一种时尚．车的使用费用，尤其是随着使用年限的增多，所支出的费用到底会增长多少，一直是购车一族非常关心的问题．某汽车销售公司作了一次抽样调查，并统计得出某款车的使用年限x与所支出的总费用y（万元）有如表的数据资料：
（1）在给出的坐标系中做出散点图；
（2）求线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中的$\widehat{a}$、$\widehat{b}$；
（3）估计使用年限为12年时，车的使用总费用是多少？
（最小二乘法求线性回归方程系数公式$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$）．
随着人们经济收入的不断增长，个人购买家庭轿车已不再是一种时尚．车的使用费用，尤其是随着使用年限的增多，所支出的费用到底会增长多少，一直是购车一族非常关心的问题．某汽车销售公司作了一次抽样调查，并统计得出某款车的使用年限x与所支出的总费用y（万元）有如表的数据资料：| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 总费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
（2）求线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中的$\widehat{a}$、$\widehat{b}$；
（3）估计使用年限为12年时，车的使用总费用是多少？
（最小二乘法求线性回归方程系数公式$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$）．
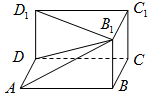长方体ABCD-A1B1C1D1被挖去一个四棱锥后如图所示．已知AB=5，BC=4，BB=3．
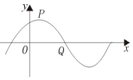已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的部分图象如图所示，其中点P（1，2）为函数图象的一个最高点，Q（4，0）为函数图象与x轴的一个交点，O为坐标原点．