题目内容
18.已知$\overrightarrow a,\overrightarrow b$是夹角为60°的两个单位向量,则当实数t∈[-1,1],$|\overrightarrow a+t\overrightarrow b|$的最大值为$\sqrt{3}$.分析 先根据向量的模和向量的数量积公式得到关于t的二次函数函数,根据函数的性质即可求出最值.
解答 解:∵$|\overrightarrow a+t\overrightarrow b|$2=|$\overrightarrow{a}$|2+t2|$\overrightarrow{b}$|2+2t|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cos60°=t2+t+1,当t=1时有最大值3,$|\overrightarrow a+t\overrightarrow b|$的最大值为$\sqrt{3}$.
故答案为:$\sqrt{3}$
点评 本题考查了向量的数量积公式和向量的模的计算,属于基础题.

练习册系列答案
相关题目
10.已知△ABC的外接圆半径为1,圆心为O,且满足$\overrightarrow{OA}+2\overrightarrow{OB}+4\overrightarrow{OC}=0$,则$\overrightarrow{AB}•\;\overrightarrow{OA}$=( )
| A. | $-\frac{15}{4}$ | B. | $-\frac{7}{4}$ | C. | $\frac{7}{4}$ | D. | $\frac{15}{4}$ |
8.已知数列{an}中,a1=-$\frac{1}{4}$,an=1-$\frac{1}{{a}_{n-1}}$(n>1),则a2016的值为( )
| A. | -$\frac{1}{4}$ | B. | 5 | C. | $\frac{4}{5}$ | D. | 2 |
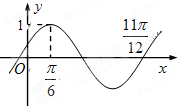 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$|的部分图象如图示,现将函数y=f(x)的图象向右平移$\frac{π}{12}$个单位后,得到函数y=g(x)的图象,则平移后得到的函数解析式g(x)=sin2x.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$|的部分图象如图示,现将函数y=f(x)的图象向右平移$\frac{π}{12}$个单位后,得到函数y=g(x)的图象,则平移后得到的函数解析式g(x)=sin2x.