题目内容
17．
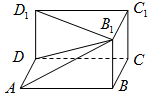长方体ABCD-A1B1C1D1被挖去一个四棱锥后如图所示．已知AB=5，BC=4，BB=3．（1）请补全此图的三视图；
（2）求此几何体的体积．
分析 （1）利用三视图的作法，画出图形即可．
（2）利用长方体的体积减去三棱锥的体积求解即可．
解答 
解：（1）三视图如右所示；
（2）几何体是长方体减去一个三棱锥得到的几何体，它的体积为：V=3×4×5$-\frac{1}{3}×\frac{1}{2}×2×3×5$=40．
点评 本题考查三视图的画法，几何体的体积的求法，判断几何体的形状是解题的关键．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
7．已知f'（x）为f（x）的导函数，若f（x）=ln$\frac{x}{2}$，且b$\int_1^b$$\frac{1}{x^3}$dx=2f'（a）+$\frac{1}{2}b}$-1，则a+b的最小值为（ ）
| A． | $4\sqrt{2}$ | B． | $2\sqrt{2}$ | C． | $\frac{9}{2}$ | D． | $\frac{9}{2}+2\sqrt{2}$ |
12．设集合A={x∈Z|x＞-1}，则（ ）
| A． | ∅∉A | B． | $\sqrt{2}$∉A | C． | $\sqrt{2}∈A$ | D． | {$\sqrt{2}$}⊆A |