题目内容
1.狄利克雷函数是高等数学中的一个典型函数,若f(x)=$\left\{\begin{array}{l}{1,x∈Q}\\{0,x∈{∁}_{R}U}\end{array}\right.$,则称f(x)为狄利克雷函数.对于狄利克雷函数f(x),给出下面4个命题:①对任意x∈R,都有f[f(x)]=1;②对任意x∈R,都有f(-x)+f(x)=0;③对任意x1∈R,都有x2∈Q,f(x1+x2 )=f(x1);④对任意a,b∈(-∞,0),都有{x|f(x)>a}={x|f(x)>b}.其中所有真命题的序号是( )| A. | ①④ | B. | ②③ | C. | ①②③ | D. | ①③④ |
分析 根据狄利克雷函数,分别讨论当x∈Q和x∈∁RQ时,对应命题是否成立即可.
解答 解:①当x∈Q,则f(x)=1,f(1)=1,则[f(x)]=1,
当x∈∁RQ,则f(x)=0,f(0)=1,则[f(x)]=1,即对任意x∈R,都有f[f(x)]=1,故①正确,
②当x∈Q,则-x∈Q,则f(-x)=1,f(x)=1,此时f(-x)=f(x),
当x∈∁RQ,则-x∈∁RQ,则f(-x)=0,f(x)=0,此时f(-x)=f(x),
即恒有f(-x)=f(x),即函数f(x)是偶函数,故②错误,
③当x1∈Q,有x2∈Q,则x1+x2∈Q,此时f(x1+x2 )=f(x1)=1;
当x1∈∁RQ,有x2∈Q,则x1+x2∈∁RQ,此时f(x1+x2 )=f(x1)=0;
综上恒有f(x1+x2 )=f(x1)成立,故③正确,
④∵f(x)≥0恒成立,∴对任意a,b∈(-∞,0),都有{x|f(x)>a}={x|f(x)>b}=R,故④正确,
故正确的命题是①③④,
故选:D
点评 本题主要考查命题的真假判断,涉及新定义,正确理解狄利克雷函数的分段函数意义是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


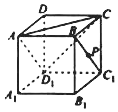 在正方体ABCD-A1B1C1D1中(如图),已知点P在直线BC1上运动.则下列四个命题:
在正方体ABCD-A1B1C1D1中(如图),已知点P在直线BC1上运动.则下列四个命题: