题目内容
5．（Ⅰ）求出函数y=x2sinx的导函数，并求f′（π）的值；（Ⅱ）求出函数y=$\frac{{e}^{x}+1}{{e}^{x}-1}$的导函数，并求f′（ln2）的值．
分析 分别先求导，再代值计算即可
解答 解：（Ⅰ）f′（x）=2xsinx+x2cosx，则f′（π）=2πsinπ+π2cosπ=-π2，
（Ⅱ）f（x）=$\frac{{e}^{x}+1}{{e}^{x}-1}$=1+$\frac{2}{{e}^{x}-1}$，
则f′（x）=-$\frac{2{e}^{x}}{（{e}^{x}-1）^{2}}$，
则f′（ln2）=-$\frac{2{e}^{ln2}}{（{e}^{ln2}-1）^{2}}$=-4．
点评 本题考查了导数的运算法则和导数值的求法，属于基础题
练习册系列答案
相关题目
15．单位正方体（棱长为1）被切去一部分，剩下部分几何体的三视图如图所示，则（ ）
| A． | 该几何体体积为$\frac{5}{6}$ | B． | 该几何体体积可能为$\frac{2}{3}$ | ||
| C． | 该几何体表面积应为$\frac{9}{2}+\frac{{\sqrt{3}}}{2}$ | D． | 该几何体表面积应为$\frac{7}{2}+\frac{{\sqrt{3}}}{2}$ |
16．
一个四棱锥的侧棱长都相等，底面是正方形，且其正视图为如图所示的等腰三角形，则该四棱锥的表面积是（ ）
一个四棱锥的侧棱长都相等，底面是正方形，且其正视图为如图所示的等腰三角形，则该四棱锥的表面积是（ ）| A． | 12 | B． | $4\sqrt{5}$ | C． | $4+4\sqrt{3}$ | D． | $4+4\sqrt{5}$ |
17．某几何体的三视图如图所示（网格中的小正方形边长为），则该几何体的体积为（ ）
| A． | $\frac{16}{3}$ | B． | $\frac{10}{3}$ | C． | $\frac{8}{3}$ |
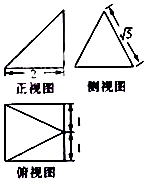
14．已知某几何体的三视图如图所示，则该几何体的体积为（ ）
| A． | $\frac{4}{3}$$\sqrt{5}$ | B． | 4$\sqrt{5}$ | C． | $\frac{8}{3}$ | D． | 8 |