题目内容
不等式22x≤3•2x+
+4•22
的解集是 .
| x |
| x |
考点:指、对数不等式的解法
专题:转化思想,不等式的解法及应用
分析:不等式即(2x-
)2-3?2x-
-4≤0,设t=2x-
,则不等式等价为t2-3?t-4≤0,解得t的范围,可得x的范围.
| x |
| x |
| x |
解答:
解:不等式式2 2x≤3•2x+
+4•22
等价于
≤
+4,
即22x-2
≤3?2x-
+4,∴(2x-
)2-3?2x-
-4≤0,
设t=2x-
,则不等式等价为t2-3?t-4≤0,解得-1≤t≤4,即-1≤2x-
≤4,
∴x-
≤2,解得-1≤
≤2,∴0≤x≤4,
故答案为:[0,4].
| x |
| x |
| 22x | ||
22
|
3?2x+
| ||
22
|
即22x-2
| x |
| x |
| x |
| x |
设t=2x-
| x |
| x |
∴x-
| x |
| x |
故答案为:[0,4].
点评:本题主要考查指数不等式的解法,体现了转化、换元的数学思想,属于中档题.

练习册系列答案
相关题目
sin15°sin105°的值是( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
 函数
函数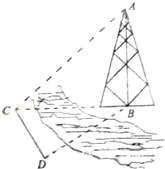 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个侧点C与D.现测得∠BCD=60°,∠BDC=75°,CD=50
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个侧点C与D.现测得∠BCD=60°,∠BDC=75°,CD=50