题目内容
已知函数y=f(x)的定义域为[0,1],则函数y=f(x+a)+f(x-a)(0<a<
)的定义域为( )
| 1 |
| 2 |
| A、φ |
| B、[a,1-a] |
| C、[-a,1+a] |
| D、[0,1] |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据复合函数定义域之间的关系进行求解即可.
解答:
解:∵函数y=f(x)的定义域为[0,1],
∴由
,
得
,
∵0<a<
,
∴1<a+1<
,-
<1-a<1
则1-a<a+1,
∴不等式组的解为a≤x≤1-a,
则函数y=f(x+a)+f(x-a)(0<a<
)的定义域为[a,1-a],
故选:B
∴由
|
得
|
∵0<a<
| 1 |
| 2 |
∴1<a+1<
| 3 |
| 2 |
| 1 |
| 2 |
则1-a<a+1,
∴不等式组的解为a≤x≤1-a,
则函数y=f(x+a)+f(x-a)(0<a<
| 1 |
| 2 |
故选:B
点评:本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
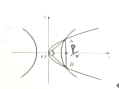
已知双曲线
-
=1(a>0,b>0)的左、右焦点分别为F1,F2,过F2向其中一条渐进线作垂线,垂足为N,已知点M在y轴上,且满足
=2
,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| F2M |
| F2N |
A、
| ||
B、
| ||
C、2
| ||
| D、2 |
某化工厂单位要在600名员工中抽取60名员工调查职工身体健康状况,其中青年员工300名,中年员工200名,老年员工100名,下列说法错误的是( )
| A、老年人应作为重点调查对象,故老年人应该抽超过30名 | ||
B、每个人被抽到的概率相同为
| ||
| C、应使用分层抽样抽取样本调查 | ||
| D、抽出的样本能在一定程度上反应总体的健康状况 |
下列不可能是函数图象的是( )
A、 |
B、 |
C、 |
D、 |
设函数f(x)=x2+2ax+b2,若a∈[0,2],b∈[0,3],则函数f(x)有零点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,双曲线
如图,双曲线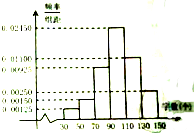 重庆Z中学为筹备参加“汉字听写比赛”,对初二年级的400名同学进行了一次摸底听写比赛,每位同学听写150个字,听写正确130个字以上(含130个)的同学才可以参加市级决赛.
重庆Z中学为筹备参加“汉字听写比赛”,对初二年级的400名同学进行了一次摸底听写比赛,每位同学听写150个字,听写正确130个字以上(含130个)的同学才可以参加市级决赛.