题目内容
8.变式已知f(x)=cos(2x+θ)关于直线x=$\frac{π}{6}$对称,求θ的值.分析 根据三角函数的对称性进行求解即可.
解答 解:∵f(x)=cos(2x+θ)关于直线x=$\frac{π}{6}$对称,
∴由2•$\frac{π}{6}$+θ=kπ,
得θ=kπ-$\frac{π}{3}$,k∈Z.
点评 本题主要考查三角函数的图象和性质,利用函数的对称性建立方程关系是解决本题的关键.比较基础.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
19.在等差数列{an}中,已知a2+a9=10.则3a5+a7=( )
| A. | 17 | B. | 18 | C. | 19 | D. | 20 |
13.执行如图的程序框图,如果输入的N=100,则输出的x=( )
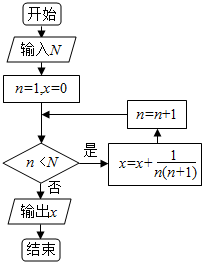

| A. | 0.95 | B. | 0.98 | C. | 0.99 | D. | 1.00 |
20.若α,β均为锐角且α+β>$\frac{π}{2}$,则( )
| A. | sinα>cosβ | B. | sinα<cosβ | C. | sinα>sinβ | D. | sinα<sinβ |
13.若椭圆和双曲线C:2x2-2y2=1有相同的焦点,且该椭圆经过点$({1,-\frac{3}{2}})$,则椭圆的方程为( )
| A. | $\frac{x^2}{5}+\frac{y^2}{4}=1$ | B. | $\frac{x^2}{4}+\frac{y^2}{3}=1$ | C. | $\frac{x^2}{4}+\frac{y^2}{5}=1$ | D. | $\frac{x^2}{9}+\frac{y^2}{5}=1$ |
 求证:分别过已知直线外一点与这条直线上的三点的三条直线共面(如图所示).
求证:分别过已知直线外一点与这条直线上的三点的三条直线共面(如图所示).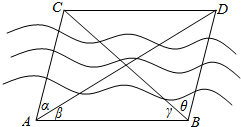 如图,为测不可到达的河北岸C,D两点间的距离,在河南岸选取A,B两点,测得AB=100m,α=β=30°,γ=45°,θ=75°,试求C,D间的距离.
如图,为测不可到达的河北岸C,D两点间的距离,在河南岸选取A,B两点,测得AB=100m,α=β=30°,γ=45°,θ=75°,试求C,D间的距离.