题目内容
20.若α,β均为锐角且α+β>$\frac{π}{2}$,则( )| A. | sinα>cosβ | B. | sinα<cosβ | C. | sinα>sinβ | D. | sinα<sinβ |
分析 根据三角函数的诱导公式以及三角函数的单调性进行转化求解即可.
解答 解:∵α,β均为锐角且α+β>$\frac{π}{2}$,
∴α>$\frac{π}{2}$-β,
即$\frac{π}{2}$>α>$\frac{π}{2}$-β>0,
∵在[0,$\frac{π}{2}$]上y=sinx是增函数,
∴sinα>sin($\frac{π}{2}$-β)=cosβ,
即sinα>cosβ,
故选:A.
点评 本题主要考查函数值的大小比较,根据三角函数的有限公司以及正弦函数的单调性是解决本题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
11.已知tan2θ=$\frac{3}{4}$,θ∈(0,$\frac{π}{4}$),则$\frac{si{n}^{2}θ+cos2θ}{sin(θ+\frac{π}{4})}$的值为( )
| A. | $\frac{9\sqrt{5}}{20}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{\sqrt{10}}{3}$ | D. | $\frac{\sqrt{10}}{10}$ |
15.设复数z满足1+i=z(2-i)(i为虚数单位),$\overline{z}$表示复数z的共扼复数,则|$\overline{z}$+$\frac{3}{5}$|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{5}$ |
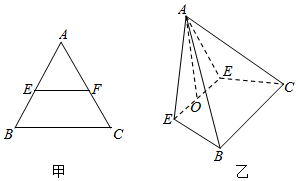 如图甲,在边长为4的等边△ABC中,点E,F分别为AB,AC上一点,且EF∥BC,EF=2a,沿EF将△AEF折起,使得平面AEF⊥平面EFCB,形成一个如图乙所示的四棱锥,设O为EF的中点.
如图甲,在边长为4的等边△ABC中,点E,F分别为AB,AC上一点,且EF∥BC,EF=2a,沿EF将△AEF折起,使得平面AEF⊥平面EFCB,形成一个如图乙所示的四棱锥,设O为EF的中点.