题目内容
ax2+bx+c=0的根的算法 .
考点:算法的特点
专题:综合题,算法和程序框图
分析:若判别式△>0,则原方程有两个不相等的实数根,若△=0,则原方程有两个相等的实数根,若△<0,则原方程无实数根;
在解方程之前,应先判断判别式的符号,再执行不同的步骤.
在解方程之前,应先判断判别式的符号,再执行不同的步骤.
解答:
解:求一元二次方程ax2+bx+c=0的根的算法步骤是
第一步,输入3个系数a,b,c;
第二步,计算△=b2-4ac;
第三步,判断△≥0是否成立,若是,则计算p=-
,q=
,否则,输出“方程没有实数根”,结束算法;
第四步,判断△=0是否成立,若是,则输出x1=x2=p,否则,计算x1=p+q,x2=p-q,并输出x1,x2.
故答案为:第一步,输入3个系数a,b,c;
第二步,计算△=b2-4ac;
第三步,判断△≥0是否成立,若是,则计算p=-
,q=
,否则,输出“方程没有实数根”,结束算法;
第四步,判断△=0是否成立,若是,则输出x1=x2=p,否则,计算x1=p+q,x2=p-q,并输出x1,x2.
第一步,输入3个系数a,b,c;
第二步,计算△=b2-4ac;
第三步,判断△≥0是否成立,若是,则计算p=-
| b |
| 2a |
| ||
| 2a |
第四步,判断△=0是否成立,若是,则输出x1=x2=p,否则,计算x1=p+q,x2=p-q,并输出x1,x2.
故答案为:第一步,输入3个系数a,b,c;
第二步,计算△=b2-4ac;
第三步,判断△≥0是否成立,若是,则计算p=-
| b |
| 2a |
| ||
| 2a |
第四步,判断△=0是否成立,若是,则输出x1=x2=p,否则,计算x1=p+q,x2=p-q,并输出x1,x2.
点评:本题考查了编写求一元二次方程ax2+bx+c=0的根的算法步骤的应用问题,是基础题目.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
函数f(x)=lgx-sinx的零点个数是( )
| A、1 | B、2 | C、3 | D、4 |
已知函数f(x)=|lg(x-1)|,若a≠b,f(a)=f(b),则a+2b的取值范围是( )
A、(4
| ||
B、[4
| ||
C、(2
| ||
D、[2
|
已知正项等比数列{an}中,Sn为其前n项和,且a2a4=1,S3=7则S5=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
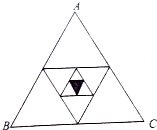 如图,等边三角形ABC,以△ABC各边中点为顶点作三角形,以此类推,现向△ABC中随机撒入320颗豆子,则落在阴影部分内的豆子大约是
如图,等边三角形ABC,以△ABC各边中点为顶点作三角形,以此类推,现向△ABC中随机撒入320颗豆子,则落在阴影部分内的豆子大约是