题目内容
已知直线y=ax+2与圆x2+y2+2x-3=0相交于A、B两点,点P(x0,y0)在直线y=2x上,且PA=PB,则x0的取值范围为 .
考点:直线与圆的位置关系
专题:直线与圆
分析:由题意可得CP垂直平分AB,且 y0=2x0.直线垂直的关系,解得x0与a的关系,把直线y=ax+2代入圆x2+y2+2x-3=0化为关于x的一元二次方程,由△>0,求得a的范围,从而可得x0的取值范围.
解答:
解:圆x2+y2+2x-3=0 即 (x+1)2+y2=4,表示以C(-1,0)为圆心,半径等于2的圆.
∵PA=PB,∴CP垂直平分AB,
∵P(x0,y0)在直线y=2x上,
∴y0=2x0.
又CP的斜率等于
,
∴
•a=-1,解得 x0=
.
把直线y=ax+2代入圆x2+y2+2x-3=0可得,(a2+1)x2+(4a+2)x+1=0.
由△=(4a+2)2-4(a2+1)>0,
即12a2+16a>0,
得a>0或a<-
.
∴-1<
<0,或 0<
<
.
故x0的取值范围为 (-1,0)∪(0,
),
故答案为:(-1,0)∪(0,
)
∵PA=PB,∴CP垂直平分AB,
∵P(x0,y0)在直线y=2x上,
∴y0=2x0.
又CP的斜率等于
| 2x0 |
| x0+1 |
∴
| 2x0 |
| x0+1 |
| -1 |
| 2a+1 |
把直线y=ax+2代入圆x2+y2+2x-3=0可得,(a2+1)x2+(4a+2)x+1=0.
由△=(4a+2)2-4(a2+1)>0,
即12a2+16a>0,
得a>0或a<-
| 4 |
| 3 |
∴-1<
| -1 |
| 2a+1 |
| -1 |
| 2a+1 |
| 3 |
| 5 |
故x0的取值范围为 (-1,0)∪(0,
| 3 |
| 5 |
故答案为:(-1,0)∪(0,
| 3 |
| 5 |
点评:本题主要考查直线和圆相交的性质,不等式的性质应用,属于中档题.利用直线和圆的位置关系结合判别式△是解决本题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
已知函数f(x)=(2k-1)x+2在R上是减函数,则实数k的取值范围为( )
A、k<-
| ||
B、k>-
| ||
C、k<
| ||
D、k>
|
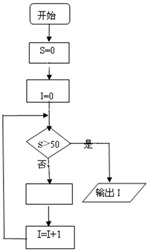 程序框图,如图所示为1+2+3+…+n>50的最小自然数n的程序框图,在空白框中应填
程序框图,如图所示为1+2+3+…+n>50的最小自然数n的程序框图,在空白框中应填