题目内容
20.已知椭圆C的中心在原点,焦点在x轴上,长轴长为4,且点$({1\;,\;\frac{{\sqrt{3}}}{2}})$在椭圆C上.(1)求椭圆C的方程;
(2)若点P在第二象限,∠F2PF1=60°,求△PF1F2的面积.
分析 (1)由题意求得a,设出椭圆方程,代入已知的坐标求得b,则椭圆方程可求;
(2)由(1)求得c及2a,在△PF1F2中,由余弦定理可得$|P{F}_{1}||P{F}_{2}|=\frac{4}{3}$,然后代入三角形面积公式可得△PF1F2的面积.
解答 解:(1)∵椭圆C的焦点在x轴上,且长轴为4,
故可设椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{b^2}=1$(a>b>0),
又点$({1\;,\;\frac{{\sqrt{3}}}{2}})$在椭圆C上,∴$\frac{1}{4}+\frac{3}{{4{b^2}}}=1$,
解得b2=1,
∴椭圆C的方程为$\frac{x^2}{4}+{y^2}=1$;
(2)由(1)知,c=$\sqrt{{a}^{2}-{b}^{2}}=\sqrt{3}$,|PF1|+|PF2|=4.
在△PF1F2中,由余弦定理可得:
$|{F}_{1}{F}_{2}{|}^{2}=|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}-2|P{F}_{1}||P{F}_{2}|cos∠{F}_{1}P{F}_{2}$,
即4c2=4a2-3|PF1||PF2|,
∴$|P{F}_{1}||P{F}_{2}|=\frac{4}{3}$.
则S=$\frac{1}{2}|P{F}_{1}||P{F}_{2}|sin60°$=$\frac{1}{2}×\frac{4}{3}×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}$.
点评 本题考查椭圆的简单性质,考查了焦点三角形中椭圆定义及余弦定理的应用,是中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
5.已知F1,F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左,右焦点,G是双曲线C上一点,且满足|GF1|-7|GF2|=0,则C经过第一象限的渐近线的斜率的取值范围是( )
| A. | (0,$\frac{\sqrt{7}}{3}$] | B. | (0,$\frac{\sqrt{5}}{2}$] | C. | ($\sqrt{2}$,$\frac{5}{3}$] | D. | ($\sqrt{2}$,$\frac{\sqrt{13}}{3}$] |
9.在△ABC中,若$|\overrightarrow{AB}|=2$,$|\overrightarrow{AC}|=3$,$|\overrightarrow{BC}|=4$,O为△ABC的内心,且$\overrightarrow{AO}=λ\overrightarrow{AB}+μ\overrightarrow{BC}$,则λ+μ=( )
| A. | $\frac{3}{4}$ | B. | $\frac{5}{9}$ | C. | $\frac{7}{9}$ | D. | $\frac{5}{7}$ |
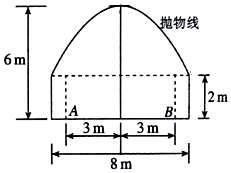 如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,已知行车道总宽度|AB|=6米,那么车辆通过隧道的限制高度是多少米?
如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,已知行车道总宽度|AB|=6米,那么车辆通过隧道的限制高度是多少米?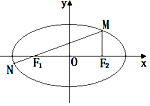 设F1,F2分别是椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右焦点,M是椭圆C上一点,且直线MF2与x轴垂直,直线MF1与C的另一个交点为N.
设F1,F2分别是椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右焦点,M是椭圆C上一点,且直线MF2与x轴垂直,直线MF1与C的另一个交点为N.