直线xcosθ+ysinθ+a=0与圆x2+y2=a2交点的个数是( )A．0B．1C．随a变化D．随θ变化题目和参考答案——青夏教育精英家教网—

题目内容

7．直线xcosθ+ysinθ+a=0与圆x²+y²=a²交点的个数是（　　）

A．

B．

C．

随a变化

D．

随θ变化

分析将圆心代入点到直线距离公式，得到圆心到直线xcosθ+ysinθ+a=0的距离d=|a|，可得结论．

解答解：圆x²+y²=a²的圆心为原点，半径为|a|，
圆心到直线xcosθ+ysinθ+a=0的距离d=|a|，
故直线与圆相切，
即直线xcosθ+ysinθ+a=0与圆x²+y²=a²交点的个数是1个，
故选：B．

点评本题考查的知识点是直线与圆的位置关系，点到直线的距离公式，难度中档．

练习册系列答案

18．定义$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc，则$|{\begin{array}{l}{sin{{50}°}}&{cos{{40}°}}\\{-\sqrt{3}tan{{10}°}}&1\end{array}}|$=（　　）

15．直线ax+by=1与圆C：x²+y²=1相切，则点P（a，b）与圆C的位置关系在圆上（填“在圆上”、“在圆外”或“在圆内”）

2．若a，b是函数y=（x²-10x+22）e^x的两个极值点，且C_n^a=C_n^b，则n的值为8．

12．.已知数列{a_n}，{b_n}满足：a_n+b_n=1，b_n+1=$\frac{b_n}{{（1-{a_n}）（1+{a_n}）}}$，且a₁，b₁是函数f（x）=16x²-16x+3的零点（a₁＜b₁）．
（1）求a₁，b₁，b₂；
（2）设c_n=$\frac{1}{{{b_n}-1}}$，求证：数列{c_n}是等差数列，并求b_n的通项公式；
（3）设S_n=a₁a₂+a₂a₃+a₃a₄+…+a_na_n+1，不等式4aS_n＜b_n恒成立时，求实数a的取值范围．

19．

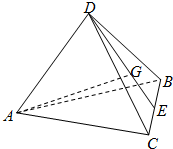如图，在四面体ABCD中，AB=1，AC=2，AD=3，∠DAB=∠DAC=60°，∠BAC=90°，G为△DBC的重心，则AG=$\frac{\sqrt{23}}{3}$．

16．

观察如图，则第（　　）行的各数之和等于2015²．

17．设m∈R，若函数y=e^x-mx在区间[1，2]的最小值为4，则m的值为e-4．

试题分类