Question

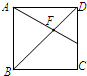如图，正方形ABCD的边长为3，E为DC的中点，AE与BD相交于F，则

FD

•

DE

的值是（　　）

• A、

  3

  2

• B、3
• C、-

  3

  2

• D、-3

Answer 1

考点：平面向量数量积的运算

专题：平面向量及应用

分析：如图所示，建立直角坐标系．由E为DC的中点，可得

BF

FD

=

AB

DE

=2．因此

FD

=

1

3

BD

．再利用数量积的坐标运算即可得出．

解答： 解：如图所示，
B（0，0，0），E(3，

3

2

)，D（3，3）．
∴

BD

=（3，3），

DE

=(0，-

3

2

)．
∴

BD

•

DE

=-

9

2

．
∵E为DC的中点，∴

BF

FD

=

AB

DE

=2．
∴

FD

=

1

3

BD

．
∴

FD

•

DE

=

1

3

BD

•

DE

=

1

3

×(-

9

2

)=-

3

2

．
故选：C．

点评：本题考查了向量的共线定理、数量积的坐标运算，属于基础题．