题目内容
下列四个不等式,正确的是( )
A、sin(-
| ||||
B、cos(-
| ||||
| C、tan318°<tan323° | ||||
| D、cos515°<cos530° |
考点:运用诱导公式化简求值
专题:三角函数的图像与性质
分析:利用诱导公式化、以及三角函数的单调性,判断各个选项是否正确,从而得出结论.
解答:
解:根据函数y=sinx在(-
,0)上是增函数,-
>-
,∴sin(-
)>sin(-
),故A不正确.
由于 cos(-
)=cos(-
)=cos
,cos(-
)=cos(-
)=cos
,
函数y=cosx在(0,π)上是减函数,
<
,∴cos
>cos
.
即 cos(-
)>cos(-
),故B不成立.
由于tan318°=tan(-42°)=-tan42°,tan323°=tan(-37°)=-tan37°,
函数y=tanx在(0°,90°)上是增函数,∴tan42°>tan37°,∴-tan42°<-tan37°,
即tan318°<tan323°,故C正确.
∵cos515°=cos155°,cos530°=cos170°,y=cosx在(0°,180°)上减增函数,
∴cos155°>cos170°,即cos515°>cos530°,故D不成立.
故选:C.
| π |
| 2 |
| π |
| 18 |
| π |
| 10 |
| π |
| 18 |
| π |
| 10 |
由于 cos(-
| 17π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 23π |
| 5 |
| 3π |
| 5 |
| 3π |
| 5 |
函数y=cosx在(0,π)上是减函数,
| π |
| 4 |
| 3π |
| 5 |
| π |
| 4 |
| 3π |
| 5 |
即 cos(-
| 17π |
| 4 |
| 23π |
| 5 |
由于tan318°=tan(-42°)=-tan42°,tan323°=tan(-37°)=-tan37°,
函数y=tanx在(0°,90°)上是增函数,∴tan42°>tan37°,∴-tan42°<-tan37°,
即tan318°<tan323°,故C正确.
∵cos515°=cos155°,cos530°=cos170°,y=cosx在(0°,180°)上减增函数,
∴cos155°>cos170°,即cos515°>cos530°,故D不成立.
故选:C.
点评:本题主要考查应用诱导公式化简三角函数式,三角函数的单调性的应用,属于基础题.

练习册系列答案
相关题目
下列有关命题的说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” |
| B、“x>2”是“x2-3x+2>0”的必要不充分条件 |
| C、命题“若x=y,则sinx=siny”的逆否命题为真命题 |
| D、命题“?x∈R使得x2+x+1<0”的否定是:“?x∈R均有x2+x+1<0” |
函数y=f(x)的图象与直线x=6的交点个数为( )
| A、至少一个 | B、至多一个 |
| C、恰好一个 | D、零个 |
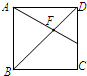 如图,正方形ABCD的边长为3,E为DC的中点,AE与BD相交于F,则
如图,正方形ABCD的边长为3,E为DC的中点,AE与BD相交于F,则| FD |
| DE |
A、
| ||
| B、3 | ||
C、-
| ||
| D、-3 |
已知曲线C1的方程为x2-
=1(x≥0,y≥0),圆C2的方程为(x-3)2+y2=1,斜率为k(k>0)的直线AB与圆C2相切于A且交C1于B.若|
|=
,则k=( )
| y2 |
| 8 |
| AB |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
计算机中常用的十六进制是逢16进1的记数制,采用数字0-9和字母A-F共16个记数符号;这些符号与十进制的数的对应关系如下表:
例如,用十六进制表示:E+D=1B,则A×E=( )
| 十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| A、6E | B、8C | C、5F | D、82 |
函数y=
在[2,3]上的最小值为( )
| 1 |
| x |
| A、2 | ||
B、
| ||
C、
| ||
D、-
|
在正方体ABCD-A1B1C1D1中,二面角A1-BD-A的正切值等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|