题目内容
13．设Sn为数列{an}的前n项和，Sn=2n2-30n．（1）求a1及an；
（2）判断这个数列是否是等差数列．
分析 （1）在数列的前n项和中，取n=1求得a1，再由an=Sn-Sn-1（n≥2）求得an；
（2）由（1）中求得的通项公式，利用定义判断数列是等差数列．
解答 解：（1）由Sn=2n2-30n，得${a}_{1}={S}_{1}=2×{1}^{2}-30×1=-28$，
当n≥2时，an=Sn-Sn-1=2n2-30n-[2（n-1）2-30（n-1）]=4n-32．
验证n=1上式成立，
∴an=4n-32；
（2）由an=4n-32，得an-1=4（n-1）-32（n≥2），
∴an-an-1=4n-32-[4（n-1）-32]=4（常数），
∴数列{an}是等差数列．
点评 本题考查等差数列的通项公式，考查了等差数列的前n项和，是基础题．
练习册系列答案
相关题目
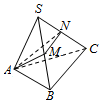如图，一个三棱锥，底面ABC为正三角形，侧棱SA=SB=SC=1，∠ASB=30°，M、N分别为棱SB和SC上的点，求△AMN的周长的最小值．
18．设函数f（x）=-x2+2x+3，x∈（-3，2]，则f（x）的值域为（ ）
| A． | （-12，3] | B． | （-12，3） | C． | （-12，4] | D． | （-12，4） |