题目内容
5.已知数列{an}的前n项为Sn,且满足关系式lg(Sn-1)=n (n∈N*),则数列{an}的通项公式an=( )| A. | 9•10n-1 | B. | $\left\{{\begin{array}{l}{11}\\{9•{{10}^{n-1}}}\end{array}\begin{array}{l}{,n=1}\\{,n≥2}\end{array}}\right.$ | ||
| C. | 10n+1 | D. | $\left\{{\begin{array}{l}9\\{{{10}^n}+1}\end{array}\begin{array}{l}{,n=1}\\{,n≥2}\end{array}}\right.$ |
分析 lg(Sn-1)=n (n∈N*),化为Sn=10n+1,利用递推关系即可得出.
解答 解:∵lg(Sn-1)=n (n∈N*),
∴Sn-1=10n,即Sn=10n+1,
当n=1时,a1=S1=11.
当n≥2时,an=Sn-Sn-1=10n+1-(10n-1+1)=•10n-1.
∴an=$\left\{\begin{array}{l}{11,n=1}\\{9•1{0}^{n-1},n≥2}\end{array}\right.$.
故选:B.
点评 本题考查了数列的通项公式、递推关系、函数的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
13.以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角形”.

该表由若干行数字组成,第一行共有2016个数字,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为( )

该表由若干行数字组成,第一行共有2016个数字,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为( )
| A. | 2016×22015 | B. | 2016×22014 | C. | 2017×22015 | D. | 2017×22014 |
20.在平面直角坐标系中,“点M的坐标满足方程4$\sqrt{x}$+y=0”是“点M在曲线y2=16x上”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
10.sin330°的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
14.下列说法正确的是( )
| A. | 长度相等的向量叫相等向量 | |
| B. | 零向量的长度为零 | |
| C. | 共线向量是在一条直线上的向量 | |
| D. | 平行向量就是向量所在的直线平行的向量 |
 如图,在三棱柱ABC-A1B1C1中,G为ABC的重心,延长线段AG交BC于F,B1F交BC1于E.
如图,在三棱柱ABC-A1B1C1中,G为ABC的重心,延长线段AG交BC于F,B1F交BC1于E.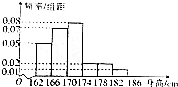 2016年高考报名体检中,某市共有40000名男生参加体检,体检其中一项为测量身高,统计调查数据显示所有男生的身高服从正态分布N(170,16).统计人员从市一中高三的参加体检的男生中随机抽取了50名进行身高测量,所得数据全部介于162cm和186cm之间,并将测量数据分成6组:第一组[162,166),第二组[166,170),…,第六组[182,186),然后按上述分组方式绘制得到如图所示的频率分布直方图.
2016年高考报名体检中,某市共有40000名男生参加体检,体检其中一项为测量身高,统计调查数据显示所有男生的身高服从正态分布N(170,16).统计人员从市一中高三的参加体检的男生中随机抽取了50名进行身高测量,所得数据全部介于162cm和186cm之间,并将测量数据分成6组:第一组[162,166),第二组[166,170),…,第六组[182,186),然后按上述分组方式绘制得到如图所示的频率分布直方图. 如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE∥AD.
如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE∥AD.