题目内容
如图：在矩形ABCD中，AB=2，BC=3，E，F分别在BC，CD上，BE=1，若| AB |
| AF |
| AE |
| BF |
考点：平面向量数量积的运算
专题：计算题
分析：将
•
=2转化为
•（
+
）=2，求出DF=1，而
•
=(
+
)•(
+
)利用向量数量积的运算法则，转化为垂直向量，平行向量的数量积．
| AB |
| AF |
| AB |
| AD |
| DF |
| AE |
| BF |
| AB |
| BE |
| BC |
| CF |
解答：
解：∵
•
=2，∴
•（
+
）=2，即
•
+
•
=2，化简2|
|=2，∴DF=1，
∴
•
=(
+
)•(
+
)=
•
+
•
+
+
=0+（-2）+3+O=1
故答案为：1
| AB |
| AF |
| AB |
| AD |
| DF |
| AB |
| AD |
| AB |
| DF |
| DF |
∴
| AE |
| BF |
| AB |
| BE |
| BC |
| CF |
| AB |
| BC |
| AB |
| CF |
| BE |
| •BC |
| BE |
| •CF |
故答案为：1
点评：本题考查向量数量积的计算，应用法则转化是关键．
练习册系列答案
相关题目
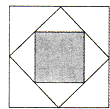任意画一个正方形，再将这个正方形各边的中点相连得到第二个正方形，依此类推，这样一共画了3个正方形，如图所示．若向图形中随机投一点，则所投点落在第三个正方形的概率是