题目内容
 如图:AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点,求证:平面PAC⊥平面PBC.
如图:AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点,求证:平面PAC⊥平面PBC.考点:平面与平面垂直的判定
专题:
分析:要证明平面PAC垂直于平面PBC,直线证明平面PBC内的直线BC,垂直平面PAC内的两条相交直线PA、AC即可.
解答:
证明:设⊙O所在平面为α,由已知条件,PA⊥α,BC在α内,
所以PA⊥BC
因为点C是圆周上不同于A、B的任意一点,AB是⊙O的直径,
所以∠BCA=90°,即BC⊥AC
又因为PA∩AC=A,所以BC⊥平面PAC
又因为BC?平面PBC,所以平面PAC⊥平面PBC.
所以PA⊥BC
因为点C是圆周上不同于A、B的任意一点,AB是⊙O的直径,
所以∠BCA=90°,即BC⊥AC
又因为PA∩AC=A,所以BC⊥平面PAC
又因为BC?平面PBC,所以平面PAC⊥平面PBC.
点评:本题考查直线与平面平行与垂直的判定,考查空间想象能力,逻辑思维能力,是基础题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
若函数f(x)=kx-lnx在区间(1,+∞)单调递增,则k的取值范围是( )
| A、(-∞,-2] |
| B、(-∞,-1] |
| C、[2,+∞) |
| D、[1,+∞) |
下列命题的说法错误的是( )
| A、命题“若x2-3x+2=0,则 x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” |
| B、若p∧q为假命题,则p,q均为假命题 |
| C、“x=1”是“x2-3x+2=0”的充分不必要条件 |
| D、对于命题p:?x∈R,x2+x+1>0,则¬p:?x∈R,x2+x+1≤0 |
如图,由三个小立方体搭成的几何体的俯视图是( )


A、 |
B、 |
C、 |
D、 |
 四棱锥A-BCDE的正视图和俯视图如图,其中正视图是等边三角形,俯视图是直角梯形.
四棱锥A-BCDE的正视图和俯视图如图,其中正视图是等边三角形,俯视图是直角梯形.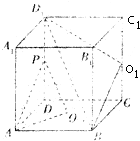 如图,在正方形ABD-A1B1C1D1,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的中点.求证:
如图,在正方形ABD-A1B1C1D1,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的中点.求证: