题目内容
 四棱锥A-BCDE的正视图和俯视图如图,其中正视图是等边三角形,俯视图是直角梯形.
四棱锥A-BCDE的正视图和俯视图如图,其中正视图是等边三角形,俯视图是直角梯形.(Ⅰ)若F为AC的中点,当点M在棱AD上移动时,是否总有BF丄CM,请说明理由.
(Ⅱ)求二面角B-AD-C的平面角的正切值.
考点:二面角的平面角及求法,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(Ⅰ)判断总有BF丄CM,可以通过取BC的中点O,连接AO,证明AO⊥CD,然后证明CD⊥面ABC,推出CD⊥BF.BF⊥AC.通过直线与平面垂直的判定定理证明BF⊥面ACD,然后说明BF丄CM.
(Ⅱ)作BH垂直于AD于H点,连HF,∠BHF即为该二面角的平面角,然后解三角形即可求二面角B-AD-C的平面角的正切值.
(Ⅱ)作BH垂直于AD于H点,连HF,∠BHF即为该二面角的平面角,然后解三角形即可求二面角B-AD-C的平面角的正切值.
解答:
解:(Ⅰ)证明:是总有BF丄CM.理由如下:
取BC的中点O,连接AO,
由俯视图可知,AO⊥平面BCDE,CD?平面BCDE,
所以AO⊥CD …(2分)
又CD⊥BC,AO∩BC=O,所以CD⊥面ABC,
因为BF?面ABC,
故CD⊥BF.
因为F是AC的中点,所以BF⊥AC.…(4分)
又AC∩CD=D
故BF⊥面ACD,
因为CM?面ACD,所以BF丄CM.…(6分)
(2)作BH垂直于AD于H点,连HF,∠BHF即为该二面角的平面角,BC=AB=AC=2,BF=
,
CD=2.AD=2
,在△AHF中,∠FAH=45°,AH⊥HF,∴HF=
,
tan∠BHF=
=
=
…(12分)
取BC的中点O,连接AO,
由俯视图可知,AO⊥平面BCDE,CD?平面BCDE,
所以AO⊥CD …(2分)
又CD⊥BC,AO∩BC=O,所以CD⊥面ABC,
因为BF?面ABC,
故CD⊥BF.
因为F是AC的中点,所以BF⊥AC.…(4分)

又AC∩CD=D
故BF⊥面ACD,
因为CM?面ACD,所以BF丄CM.…(6分)
(2)作BH垂直于AD于H点,连HF,∠BHF即为该二面角的平面角,BC=AB=AC=2,BF=
| 3 |
CD=2.AD=2
| 2 |
| ||
| 2 |
tan∠BHF=
| BF |
| HF |
| ||||
|
| 6 |
点评:本题考查直线与平面垂直的判定定理以及性质定理的应用,二面角的求法,考查空间想象能力以及转化思想的应用.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
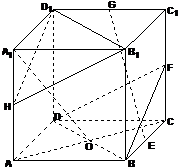 正方体ABCD-A1B1C1D1中,F,H分别为棱CC1,AA1的中点,O为AC与BD的交点.
正方体ABCD-A1B1C1D1中,F,H分别为棱CC1,AA1的中点,O为AC与BD的交点. 如图:已知PA⊥平面ABC,AB是⊙O的直径,C是圆上的任意一点,求证:PC⊥BC.
如图:已知PA⊥平面ABC,AB是⊙O的直径,C是圆上的任意一点,求证:PC⊥BC. 如图:AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点,求证:平面PAC⊥平面PBC.
如图:AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点,求证:平面PAC⊥平面PBC.