题目内容
18.已知a>0且a≠1,关于x的方程|ax-1|=5a-4有两个相异实根,则a的取值范围是$(\frac{4}{5},1)$.分析 先画出a>1和0<a<1时的两种图象,根据图象可直接得出答案.
解答 解:据题意,函数y=|ax-1|(a>0,a≠1)的图象与直线y=5a-4有两个不同的交点.
当a>1时,0<5a-4<1,所以a∈($\frac{4}{5}$,1),舍去.
当0<a<1时
由图知,0<5a-4<1,所以a∈($\frac{4}{5}$,1),
故答案为:$(\frac{4}{5},1)$.
点评 本题主要考查指数函数的图象,对于指数函数的图象要分两种情况来考虑,即a>1和0<a<1.属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.设F1,F2分别是椭圆$E:{x^2}+\frac{y^2}{b^2}=1(0<b<1)$的左、右焦点,已知点F1的直线交椭圆E于A,B两点,若|AF1|=2|BF1|,AF2⊥x轴,则椭圆E的方程为( )
| A. | ${x^2}+\frac{{3{y^2}}}{2}=1$ | B. | ${x^2}+\frac{{6{y^2}}}{5}=1$ | C. | ${x^2}+\frac{{5{y^2}}}{4}=1$ | D. | ${x^2}+\frac{{8{y^2}}}{7}=1$ |
13.执行图的程序框图后,输出的结果为( )
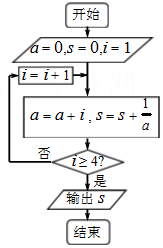

| A. | $\frac{8}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
3.如图所示,正方体ABCD-A′B′C′D′的棱长为1,O是平面A′B′C′D′的中心,则O到平面ABC′D′的距离是( )
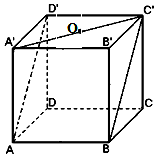

| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
