题目内容
2.点P(-1,2)到直线3x-4y+12=0的距离为( )| A. | 5 | B. | $\frac{1}{5}$ | C. | 1 | D. | 2 |
分析 利用点到直线的距离公式即可得出.
解答 解:点P(-1,2)到直线3x-4y+12=0的距离d=$\frac{|-3-8+12|}{\sqrt{{3}^{2}+(-4)^{2}}}$=$\frac{1}{5}$.
故选:B.
点评 本题考查了点到直线的距离公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
12.在区间(1,2)内随机取个实数a,则直线y=2x,直线x=a与x轴围成的面积大于$\frac{16}{9}$的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
13.执行图的程序框图后,输出的结果为( )
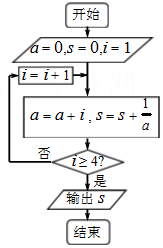

| A. | $\frac{8}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
6.已知条件p:k=$\sqrt{3}$;条件q:直线y=kx+2与圆x2+y2=1相切,则¬p是¬q的( )
| A. | 充分必要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
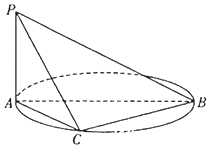 如图,AB是圆O的直径,PA垂直圆所在的平面,C是圆上的点.
如图,AB是圆O的直径,PA垂直圆所在的平面,C是圆上的点.