题目内容
15.已知四棱锥P-ABCD的正视图1是一个底边长为4、腰长为3的等腰三角形,图2、图53分别是四棱锥P-ABCD的侧视图和俯视图.(1)求证:AD⊥PC;
(2)求四棱锥P-ABCD的侧面积.
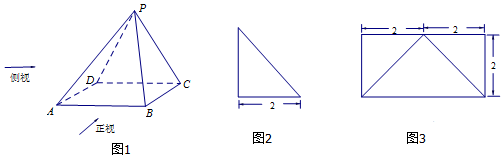
分析 (1)根据三视图形状可得侧面PDC⊥平面ABCD,结合矩形ABCD中AD⊥CD,由面面垂直的性质得AD⊥侧面PDC.再根据线面垂直的性质,结合PC?侧面PDC可证出AD⊥PC;
(2)过E作EF⊥AB,垂足为F,连接PF,分别求出侧面积,即得四棱锥P-ABCD的侧面积.
解答 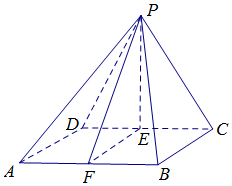 (1)证明:依题意,可知点P在平面ABCD上的正射影是线段CD的中点E,连接PE,
(1)证明:依题意,可知点P在平面ABCD上的正射影是线段CD的中点E,连接PE,
则PE⊥平面ABCD.…(1分)
∵AD?平面ABCD,
∴AD⊥PE.…(2分)
∵AD⊥CD,CD∩PE=E,CD?平面PCD,PE?平面PCD,
∴AD⊥平面PCD.…(4分)
∵PC?平面PCD,
∴AD⊥PC.…(5分)
(2)解:依题意,在等腰三角形PCD中,PC=PD=3,DE=EC=2,
在Rt△PED中,$PE=\sqrt{P{D^2}-D{E^2}}=\sqrt{5}$,…(6分)
过E作EF⊥AB,垂足为F,连接PF,
∵PE⊥平面ABCD,AB?平面ABCD,
∴AB⊥PE.
∵EF?平面PEF,PE?平面PEF,EF∩PE=E,
∴AB⊥平面PEF.
∵PF?平面PEF,
∴AB⊥PF.
依题意得EF=AD=2.
在Rt△PEF中,$PF=\sqrt{P{E^2}+E{F^2}}=3$,…(9分)
∴四棱锥P-ABCD的侧面积
$\begin{array}{l}{S_{△PAB}}+{S_{△PBC}}+{S_{△PCD}}+{S_{△PAD}}=\frac{1}{2}×4×3+2×\frac{1}{2}×2×3+\frac{1}{2}×4×\sqrt{5}\\=12+2\sqrt{5}\end{array}$.…(12分)
点评 本题给出三视图,要求我们证明线线垂直并求侧面三角形的面积,着重考查了三视图求面积和面面垂直、线面垂直的性质定理等知识,属于中档题.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案| A. | 2$\sqrt{6}$ | B. | 3$\sqrt{6}$ | C. | 2 | D. | 5$\sqrt{6}$ |

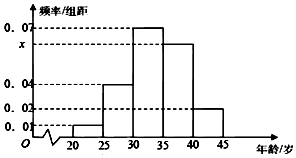 为增强市民的节能环保意识,郑州市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示,其中年龄分组区是:[20,25],[25,30],[30,35],[35,40],[40,45].
为增强市民的节能环保意识,郑州市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示,其中年龄分组区是:[20,25],[25,30],[30,35],[35,40],[40,45].