题目内容
7.已知点P在边长为2的正方形ABCD边界上运动,点M在以P为圆心,1为半径的圆上运动,则$\overrightarrow{MA}$•$\overrightarrow{MC}$的最大值为1+2$\sqrt{2}$.分析 以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,建立直角坐标系,可得A,B,C,D的坐标,设M(m,n),运用数量积的坐标表示可得$\overrightarrow{MA}$•$\overrightarrow{MC}$=m(m-2)+n(n-2)=(m-1)2+(n-1)2-2,运用几何意义:距离的平方,即可得到所求最大值.
解答 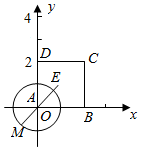 解:以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,
解:以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,
建立直角坐标系,可得A(0,0),B(2,0),C(2,2),D(0,2),
设M(m,n),则$\overrightarrow{MA}$•$\overrightarrow{MC}$=(-m,-n)•(2-m,2-n)=m(m-2)+n(n-2)
=(m-1)2+(n-1)2-2
要求$\overrightarrow{MA}$•$\overrightarrow{MC}$的最大值,
即求点(m,n)与点E(1,1)的距离的平方的最大值.
由图象可得,当P在点A,B,C,D时,连接PE,延长交圆于M,即为所求.
此时,|PM|=1+$\sqrt{2}$,
即有$\overrightarrow{MA}$•$\overrightarrow{MC}$的最大值为(1+$\sqrt{2}$)2-2=1+2$\sqrt{2}$.
故答案为:1+2$\sqrt{2}$.
点评 本题考查向量的数量积的最值的求法,考查坐标法的运用以及点与圆的位置关系,考查化简整理的运算能力,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
17.有7位歌手(1至7号)参加一场歌唱比赛,由550名大众评委现场投票决定歌手名次,根据年龄将大众评委分为5组,各组的人数如下:
(Ⅰ) 为了调查大众评委对7位歌手的支持状况,现用分层抽样方法从各组中抽取若干评委,其中从B组中抽取了6人.请将其余各组抽取的人数填入表.
(Ⅱ) 在(Ⅰ)中,若A,C两组被抽到的评委中各有2人支持1号歌手,现从这两组被抽到的评委中分别任选1人,求这2人都支持1号歌手的概率.
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 200 | 150 | 50 |
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 200 | 150 | 50 |
| 抽取人数 | 6 |
15.若复数z满足$\frac{z}{1-i}=i$,其中i为虚数单位,则z=( )
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
12.设复数z1=-1+3i,z2=1+i,则$\frac{{{z}_{1}+z}_{2}}{{z}_{1}-{z}_{2}}$=( )
| A. | -1-i | B. | 1+i | C. | 1-i | D. | -1+i |
19.设f(z)=$\overline{z}$,且z1=1+5i,z2=-3+2i.则f$\overline{({z}_{1}-{z}_{2})}$的值是( )
| A. | -2+3i | B. | -2-3i | C. | 4-3i | D. | 4+3i |
17.已知$\overrightarrow a=(cosx,-2),\overrightarrow b=(sinx,1)$且$\overrightarrow a$∥$\overrightarrow b$,则sin2x=( )
| A. | $-\frac{4}{5}$ | B. | -3 | C. | 3 | D. | $\frac{4}{5}$ |
