题目内容
 如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF=
如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF=| 1 |
| 2 |
(1)求证:BF∥平面ACE;
(2)求证:平面EAC⊥平面BDEF
(3)求几何体ABCDEF的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)记AC与BD的交点为O,则DO=BO=
BD,连接EO,则可证出四边形EFBO是平行四边形,从而BF∥EO,最后结合线面平行的判定定理,可得BF∥平面ACE;
(2)利用面面垂直的判定定理证明平面EAC⊥平面BDEF;
(3)利用条件公式求几何体的条件.
| 1 |
| 2 |
(2)利用面面垂直的判定定理证明平面EAC⊥平面BDEF;
(3)利用条件公式求几何体的条件.
解答:
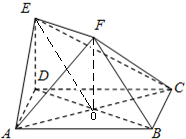 (1)证明:记AC与BD的交点为O,则DO=BO=
(1)证明:记AC与BD的交点为O,则DO=BO=
BD,连接EO,
∵EF∥BD且EF=
BD,
∴EF∥BO且EF=BO,则四边形EFBO是平行四边形,
∴BF∥EO,
又∵EO?面ACE,BF?面ACE,
∴BF∥平面ACE;
(2)证明:∵ED⊥平面ABCD,AC?平面ABCD,∴ED⊥AC.
∵ABCD为正方形,∴BD⊥AC,
又ED∩BD=D,∴AC⊥平面BDEF,
又AC?平面EAC,∴平面EAC⊥平面BDEF;
(3)解:∵ED⊥平面ABCD,∴ED⊥BD,
又∵EF∥BD且EF=
BD,∴BDEF是直角梯形,
又∵ABCD是边长为2的正方形,BD=2
,EF=
,
∴梯形BDEF的面积为
=
,
由(1)知AC⊥平面BDEF,
∴几何体的体积VABCDEF=2VA-BDEF=2×
SBDEF•AO=2×
×
×
=2.
 (1)证明:记AC与BD的交点为O,则DO=BO=
(1)证明:记AC与BD的交点为O,则DO=BO=| 1 |
| 2 |
∵EF∥BD且EF=
| 1 |
| 2 |
∴EF∥BO且EF=BO,则四边形EFBO是平行四边形,
∴BF∥EO,
又∵EO?面ACE,BF?面ACE,
∴BF∥平面ACE;
(2)证明:∵ED⊥平面ABCD,AC?平面ABCD,∴ED⊥AC.
∵ABCD为正方形,∴BD⊥AC,
又ED∩BD=D,∴AC⊥平面BDEF,
又AC?平面EAC,∴平面EAC⊥平面BDEF;
(3)解:∵ED⊥平面ABCD,∴ED⊥BD,
又∵EF∥BD且EF=
| 1 |
| 2 |
又∵ABCD是边长为2的正方形,BD=2
| 2 |
| 2 |
∴梯形BDEF的面积为
(
| ||||
| 2 |
3
| ||
| 2 |
由(1)知AC⊥平面BDEF,
∴几何体的体积VABCDEF=2VA-BDEF=2×
| 1 |
| 3 |
| 1 |
| 3 |
3
| ||
| 2 |
| 2 |
点评:本题以一个特殊多面体为例,考查了线面平行的判定定理、面面垂直的判定理、空间几何体的体积,要求熟练掌握相应的判定定理,属于中档题.

练习册系列答案
相关题目
 已知A、B、C、D四点不共面,M、N分别是△ABD和△BCD的重心.求证:MN∥平面ACD.
已知A、B、C、D四点不共面,M、N分别是△ABD和△BCD的重心.求证:MN∥平面ACD. 如图,AB是圆O的直径,PA垂直于圆所在的平面,C是圆周上的点.
如图,AB是圆O的直径,PA垂直于圆所在的平面,C是圆周上的点. 如图,已知抛物线的方程为x2=2py(p>0),过点A(0,-1)作直线l与抛物线相交于P,Q两点,点B的坐标为(0,1),连接BP,BQ,设QB,BP与x轴分别相交于M,N两点.如果QB的斜率与PB的斜率的乘积为-3,则∠MBN的大小等于
如图,已知抛物线的方程为x2=2py(p>0),过点A(0,-1)作直线l与抛物线相交于P,Q两点,点B的坐标为(0,1),连接BP,BQ,设QB,BP与x轴分别相交于M,N两点.如果QB的斜率与PB的斜率的乘积为-3,则∠MBN的大小等于