题目内容
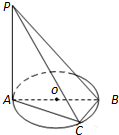 如图,AB是圆O的直径,PA垂直于圆所在的平面,C是圆周上的点.
如图,AB是圆O的直径,PA垂直于圆所在的平面,C是圆周上的点.(1)求证:平面PAC⊥平面PBC;
(2)若AB=2
| 2 |
考点:与二面角有关的立体几何综合题,平面与平面垂直的判定
专题:空间角
分析:(1)由圆的性质得AC⊥BC,由线面垂直得PA⊥BC,从而BC⊥平面PAC,由此能证明平面PBC⊥平面PAC.
(2)连接CO,过O在平面PAB上作OM⊥PB于M,连接CM,∠OMC是二面角C-PB-A的平面角,由此能求出二面角C-PB-A的度数.
(2)连接CO,过O在平面PAB上作OM⊥PB于M,连接CM,∠OMC是二面角C-PB-A的平面角,由此能求出二面角C-PB-A的度数.
解答:
(1)证明:由AB是圆O的直径,得AC⊥BC,(1分)
由PA⊥平面ABC,BC?平面ABC,得PA⊥BC,(3分)
又PA∩AC=A,∴BC⊥平面PAC,(4分)
又BC?平面PBC,
∴平面PBC⊥平面PAC.(6分)
(2)解:连接CO,∵AB=2
,
AC=2,∴BC=2,∴AB⊥OC,(8分)
过O在平面PAB上作OM⊥PB于M,连接CM,
由三垂线定理CM⊥PB,
∴∠OMC是二面角C-PB-A的平面角,(10分)
∵OC是圆半径,∴OC=
,
由△BOM∽△BPA,得OM=
,
在Rt△OMC中,tan∠OMC=
=
,
∴∠OMC=60°.
∴二面角C-PB-A的度数为60°.(12分)
由PA⊥平面ABC,BC?平面ABC,得PA⊥BC,(3分)
又PA∩AC=A,∴BC⊥平面PAC,(4分)

又BC?平面PBC,
∴平面PBC⊥平面PAC.(6分)
(2)解:连接CO,∵AB=2
| 2 |
AC=2,∴BC=2,∴AB⊥OC,(8分)
过O在平面PAB上作OM⊥PB于M,连接CM,
由三垂线定理CM⊥PB,
∴∠OMC是二面角C-PB-A的平面角,(10分)
∵OC是圆半径,∴OC=
| 2 |
由△BOM∽△BPA,得OM=
| ||
|
在Rt△OMC中,tan∠OMC=
| OC |
| OM |
| 3 |
∴∠OMC=60°.
∴二面角C-PB-A的度数为60°.(12分)
点评:本题考查平面与平面垂直的证明,考查二面角的度数的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥平面ABCD,PA=AB,∠ABC=60°,E、F分别是PB,CD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥平面ABCD,PA=AB,∠ABC=60°,E、F分别是PB,CD的中点. 如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF=
如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF= 如图,点P为矩形ABCD所在平面外一点,PA⊥平面ABCD,Q为线段AP的中点,AB=3,BC=4,PA=2,则P到平面BQD的距离为
如图,点P为矩形ABCD所在平面外一点,PA⊥平面ABCD,Q为线段AP的中点,AB=3,BC=4,PA=2,则P到平面BQD的距离为