函数y=sinx+tanx.x∈[-$\frac{π}{4}$.$\frac{π}{4}$]的值域是( )A．[-$\frac{\sqrt{2}}{2}$.$\frac{\sqrt{2}}{2}$]B．[-2.2]C．[-$\frac{\sqrt{2}}{2}$-1.$\frac{\sqrt{2}}{2}$]D．[-$\frac{\sqrt{2}}{2}$-1.$\frac{\sqrt 题目和参考答案——青夏教育精英家教网—

题目内容

18．函数y=sinx+tanx，x∈[-$\frac{π}{4}$，$\frac{π}{4}$]的值域是（　　）

A．

[-$\frac{\sqrt{2}}{2}$，$\frac{\sqrt{2}}{2}$]

B．

[-2，2]

C．

[-$\frac{\sqrt{2}}{2}$-1，$\frac{\sqrt{2}}{2}$]

D．

[-$\frac{\sqrt{2}}{2}$-1，$\frac{\sqrt{2}}{2}$+1]

分析直接利用函数的单调性求得函数值域．

解答解：∵函数y=sinx+tanx在x∈[-$\frac{π}{4}$，$\frac{π}{4}$]上为增函数，
∴${y}_{min}=-\frac{\sqrt{2}}{2}-1$，${y}_{max}=\frac{\sqrt{2}}{2}+1$．
故选：D．

点评本题考查函数值域的求法，训练了利用函数单调性求函数的值域，是基础题．

练习册系列答案

考点集训与满分备考系列答案

课堂小测6分钟系列答案

名师金手指领衔课时系列答案

期末满分冲刺阶段练习与单元测试系列答案

一线名师提优作业本加期末总复习系列答案

同步训练内蒙古大学出版社系列答案

9．已知正方体ABCD-A₁B₁C₁D₁中，E，F分别是A₁D₁，D₁C₁的中点，则异面直线EF与AB₁所成角为（　　）

6．函数y=x³cosx，x∈（-$\frac{π}{2}$，$\frac{π}{2}$）的大致图象是（　　）

13．已知函数$f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，0＜ϕ＜\frac{π}{2}）$的图象经过三点$（{0，\frac{1}{8}}），（{\frac{5}{12}，0}），（{\frac{11}{12}，0}）$，在区间$（{\frac{5}{12}，\frac{11}{12}}）$内有唯一的最小值．
（Ⅰ）求出函数f（x）=Asin（ωx+ϕ）的解析式；
（Ⅱ）求函数f（x）在R上的单调递增区间和对称中心坐标．

3．

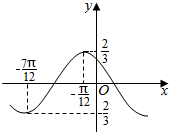函数f（x）=Asin（ωx+φ），（A＞0，ω＞0，0＜φ＜π）图象的一段如图所示
（1）求此函数的解析式；
（2）求函数f（x）在区间$[0，\frac{π}{2}]$上的最大值和最小值．

10．（1）求值：（$\frac{1}{co{s}^{2}80°}$-$\frac{3}{co{s}^{2}10°}$）•$\frac{1}{cos20°}$；
（2）已知α、β是锐角，cosα=$\frac{4}{5}$，tan（α-β）=-$\frac{1}{3}$，求cosβ的值．

7．已知数列{a_n}与{b_n}满足b_n+1-b_n=3（a_n+1-a_n），n∈N^*，在数列{a_n}中，a_n=$\frac{{n}^{2}}{3}$-16n，设数列{b_n}中的最小项是第k项，则k等于（　　）

8．在数列{a_n}中，a_n=（2n-1）3ⁿ，a₁=3，求数列的前n项和．

试题分类