题目内容
8.在空间直角坐标系中,已知点A(1,0,2),B(2,1,0),C(0,a,1),若AB⊥AC,则实数a的值为-1.分析 先利用空间向量坐标运算法则得到$\overrightarrow{AB}$=(1,1,-2),$\overrightarrow{AC}$=(-1,a,-1),再由向量垂直的性质能求出a.
解答 解:A(1,0,2),B(2,1,0),C(0,a,1),
$\overrightarrow{AB}$=(1,1,-2),$\overrightarrow{AC}$=(-1,a,-1),
∵AB⊥AC,
∴$\overrightarrow{AB}•\overrightarrow{AC}$=-1+a+2=0,
解得a=-1.
故答案为:-1.
点评 本题考查空数值的求法,是基础题,解题时要认真审题,注意向量垂直的性质的合理运用.

练习册系列答案
相关题目
18.已知命题p:若a>|b|,则a2>b2,命题q:若x2=4,则x=2,则下列命题中为真命题的是( )
| A. | p∧q | B. | p∨q | C. | ¬p | D. | q |
3.在空间直角坐标系中,点P(1,2,-3)关于坐标平面xOy的对称点为( )
| A. | (-1,-2,3) | B. | (-1,-2,-3) | C. | (-1,2,-3) | D. | (1,2,3) |
13. 如图,在四边形ABCD中,AD=DC=CB=1,$AB=\sqrt{3}$,对角线$AC=\sqrt{2}$.将△ACD沿AC所在直线翻折,当AD⊥BC时,线段BD的长度为$\sqrt{2}$.
如图,在四边形ABCD中,AD=DC=CB=1,$AB=\sqrt{3}$,对角线$AC=\sqrt{2}$.将△ACD沿AC所在直线翻折,当AD⊥BC时,线段BD的长度为$\sqrt{2}$.
 如图,在四边形ABCD中,AD=DC=CB=1,$AB=\sqrt{3}$,对角线$AC=\sqrt{2}$.将△ACD沿AC所在直线翻折,当AD⊥BC时,线段BD的长度为$\sqrt{2}$.
如图,在四边形ABCD中,AD=DC=CB=1,$AB=\sqrt{3}$,对角线$AC=\sqrt{2}$.将△ACD沿AC所在直线翻折,当AD⊥BC时,线段BD的长度为$\sqrt{2}$.
18.在等差数列{an}中,若a3+a4+a5+a6+a7=45,那么a5等于( )
| A. | 4 | B. | 5 | C. | 9 | D. | 18 |
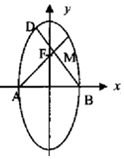 已知椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0),F为椭圆是上焦点,点A,B分别为椭圆的左右顶点,过点B作AF的垂线,垂足为N.
已知椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0),F为椭圆是上焦点,点A,B分别为椭圆的左右顶点,过点B作AF的垂线,垂足为N.