题目内容
17.已知-9,a1,a2,-1成等差数列,1,b1,b2,27成等比数列,则$\frac{b_2}{b_1}•({a_2}-{a_1})$=8.分析 由-9,a1,a2,-1成等差数列,得d=a2-a1=$\frac{8}{3}$,由1,b1,b2,27成等比数列,得q=$\frac{{b}_{2}}{{b}_{1}}$=3,由此能求出$\frac{b_2}{b_1}•({a_2}-{a_1})$的值.
解答 解:∵-9,a1,a2,-1成等差数列,
∴-9+3d=-1,解得d=$\frac{8}{3}$,∴a2-a1=$\frac{8}{3}$,
∵1,b1,b2,27成等比数列,
∴1×q3=27,解得q=3,∴$\frac{{b}_{2}}{{b}_{1}}$=3,
∴$\frac{b_2}{b_1}•({a_2}-{a_1})$=3×$\frac{8}{3}$=8.
故答案为:8.
点评 本题考查等比数列的公比与等差数列的公差的乘积的求法,是基础题,解题时要认真审题,注意等差数列与等比数列的性质的合理运用.

练习册系列答案
相关题目
7.下列条件中,能判断两个平面平行的是( )
| A. | 一个平面内的两条直线平行于另一个平面 | |
| B. | 一个平面内的无数条直线平行于另一个平面 | |
| C. | 平行于同一个平面的两个平面 | |
| D. | 垂直于同一个平面的两个平面 |
5.直线y=x-4与曲线y=$\sqrt{2x}$及x轴所围成图形的面积是( )
| A. | $\frac{64}{3}$ | B. | $\frac{40}{3}$ | C. | $\frac{56}{3}$ | D. | $\frac{38}{3}$ |
12.已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若A=60°,c=6,a=6,则此三角形有( )
| A. | 两解 | B. | 一解 | C. | 无解 | D. | 无穷多解 |
9.已知O为坐标原点,双曲线${x^2}-\frac{y^2}{b^2}=1({b>0})$上有一点P,过点P作两条渐近线的平行线,与两条渐近线的交点分别为A,B,若平行四边形PAOB的面积为1,则双曲线的离心率为( )
| A. | $\sqrt{17}$ | B. | $\sqrt{15}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
8.如图一段程序执行后输出结果是( )
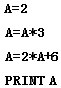
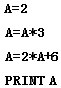
| A. | 2 | B. | 8 | C. | 18 | D. | 10 |